This is a quick test of whether Word successfully exports its own inline equations to the Web, after I was informed that inline MathType equations weren’t exported.

One thing which never ceases to bemuse me is the intellectual insularity of mainstream economics.

Every intellectual specialization is, by necessity, insular. Specialization necessarily requires that, to have expert knowledge in one field—say, physics—you must focus on that field to the exclusion of others—for example, chemistry. Given the extent of human knowledge today, this goes far further than it did in the 19^th century: the days of the true polymath are well and truly over. There are now specializations within each field, so that a physicist specializing in statistical mechanics will know relatively little about condensed matter physics, for example, and so on in other fields.

But the insularity of mainstream economics goes far beyond this necessary minimum. Though there are a few convenient exceptions who are trotted out to counter generalizations like I am making here, in general, Neoclassicals are blithely unaware of how their own school of thought developed, of empirical and theoretical results that contradict core tenets their own beliefs, of the competing schools of thought within economics, of the development of economics itself over time, and crucially, of intellectual developments that have extended human knowledge in fundamental ways that affect all fields of knowledge—including economics. Foremost here is their ignorance of complexity analysis, which has transformed many fields of study since its re-discovery in meteorology by Edward Lorenz in 1963 (Lorenz 1963).

1. Complexity
   

Complexity is often defined by what it is not, so I will attempt a positive definition—which even so, still contains a negative:

A complex system is an often very simple dynamic system which, under certain very common conditions—nonlinear interactions between some of its three or more variables—generates extremely complicated far-from-equilibrium behaviour, which cannot be understood by reducing the system to its component parts (i.e., by reductionism).

Taking each element of this definition in turn:

• A complex system is not necessarily complicated: Lorenz’s model, which I will discuss shortly, has just three equations and three parameters. Compare that to Ireland’s model, with 10 equations and 14 parameters. Lorenz’s model generates complex dynamics, while Ireland’s far more complicated model does not;
• The conditions that generate them are very common because in essence, everything is nonlinear. Even a straight line is nonlinear because, unless it starts on one side of the Universe and ends on the other, the very fact that it stops is a nonlinearity. More to the point, an economic system has numerous instances where one variable is multiplied by another—for example, the wage bill is equal to the wage rate (a variable) multiplied by the number of employees (another variable);
• Nonlinearity is essential, because effects like, for example, multiplying one variable by another, amplify disturbances. In linear models, as Blanchard himself pointed out, all effects are additive: a shock twice as big causes twice as big a disturbance. Nothing amplifies anything else;
• Three or more variables are needed because, in the type of mathematics which is used to describe complex systems, the dimensionality of the model is equal to the number of variables, and the path your system draws cannot intersect itself. A one-variable system maps to a line, and along a line you can go left, right, or towards the middle without generating the same number twice, but that’s it. A two-variable system maps to a rectangle, and you can either spiral in towards its centre, or spiral in (or out) towards a fixed orbit, but that’s it. With a three-variable system, the dynamics maps to a box, and in a box you can weave incredibly complicated patterns without ever intersecting your path;
• Far-from-equilibrium behaviour occurs because in such a system, given realistic parameters and initial conditions, one or more of the system’s equilibria can be what are called “strange attractors”: they attract the system from a distance, only to repel it when it gets near the equilibrium. Lorenz’s model has two “strange attractors”, while the economic model that I explain in Chapter 7—and which I first built in 1992—has one (Keen 1995); and
• Reductionism can’t be used to understand such a model because, as soon as you reduce the system to one (or even two) of its components, the third dimension, which is essential for its complex dynamics, is eliminated.

The great French mathematician Henri Poincare discovered the first complex system when he solved the “three body problem” in 1889, but this was long before humanity developed the capacity to visualise such systems using computers. Though he became rightly famous for solving the three-body problem, his discovery of complexity languished until the phenomenon was rediscovered by the mathematical meteorologist Edward Lorenz in 1963 (Lorenz 1963).

Lorenz was dissatisfied with the weather modelling practices of the late 1950s, which boiled down to both pattern matching (looking for a set of weather events in the past that resembled the pattern of the last few days, and predicting that tomorrow’s weather would be the same as the next day in the historical record) and linear modelling—the practice which, as Blanchard explained in “Where Danger Lurks” (Blanchard 2014), still dominates mainstream macroeconomics today.

Lorenz decided to construct an extremely simplified model of fluid dynamics which preserved the essential nonlinearity of the weather, by reducing the extremely complicated, high-dimensional Navier-Stokes partial-differential equations to just three very simple ordinary differential equations. What he saw ultimately transformed not only meteorology, but almost every field of science. But it has had virtually no impact on economics.

A picture, as they say, is worth 1000 words, so Figure 4 shows a picture of Lorenz’s model (Lorenz 1963)—rendered in the Open-Source system dynamics program Minsky, which I have developed to enable complex systems modelling in economics.

Figure 4: Lorenz’s “strange attractor” model of turbulent flow

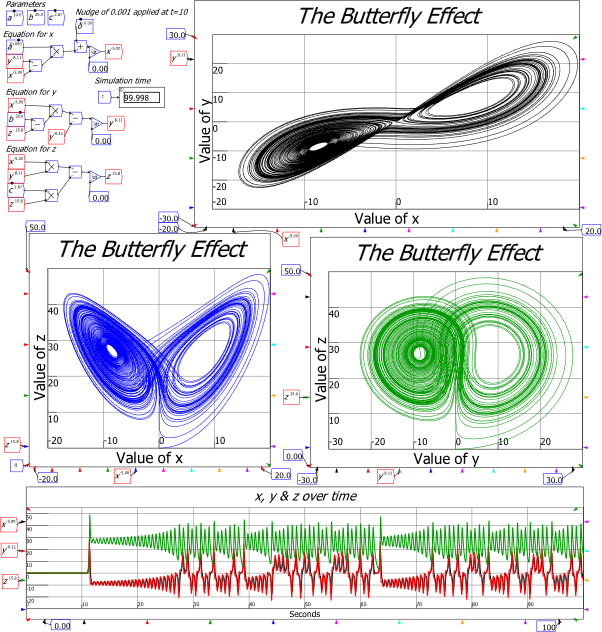
The system has just three variables (x, y and z) and three parameters (a, b, and c) and just two nonlinear interactions: in the equation for y, x is multiplied by minus z, and in the equation for z, x is multiplied by y—see Equation :

        

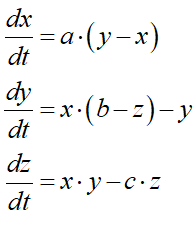
And yet, despite this simplicity, the pattern generated by the system is incredibly complicated—and indeed, beautiful. It was called “The Butterly Effect” for more reasons than one.

It could also have been called “The Mask of Zorro”, given the existence of two “eyes” in the phase plots for x against y, y against z, and z against x. Tellingly for equilibrium-obsessed economists, these eyes are in fact two of the three equilibria of the system. The third is where , which were the initial condition of the simulation shown in Figure 4. I then nudged the x-value 0.001 away from its equilibrium at the ten second mark. After this disturbance, the system was propelled away from this unstable equilibrium towards the other two—the “eyes” in the three phase plots. These equilibria are “strange attractors”, which means that they describe regions that the system will never reach—even though they are also equilibria of the system.

This simulation shows that all three equilibria of Lorenz’s system are unstable: if the system starts at an equilibrium, it will remain there, but if it starts anywhere else, or is disturbed from the equilibrium eve by an infinitesimal distance, it will be propelled away from it, and forever display far-from-equilibrium dynamics.

And yet it does not “break down”: the simulation returns realistic values that stay within the bounds of the system. This contrasts strongly with the presumption once expressed by Hicks in relation to Harrod’s “knife-edge” model of economic instability (Harrod 1939, 1948), that models must assume stable equilibria, because a model with an unstable equilibrium “does not fluctuate; it just breaks down”:

Mr. Harrod … welcomes the instability of his system, because he believes it to be an explanation of the tendency to fluctuation which exists in the real world… But mathematical instability does not in itself elucidate fluctuation. A mathematically unstable system does not fluctuate; it just breaks down. (Hicks 1949, p. 108)

This still prevalent belief amongst economists is only true of linear systems—and even then, not all of them (Keen 2020). But it is categorically false about the behaviour of nonlinear systems.

Finally, not only is the pattern beautiful, it is also aperiodic: no one cycle is like any other. Before Lorenz’s work, scientists thought that aperiodic cycles would require exogenous shocks; after Lorenz’s work, only economists continue to assume that random shocks to a system are needed to cause aperiodicity.

It is to the great credit of meteorology that, very rapidly, Lorenz’s demonstration of the necessity of nonlinear, far-from-equilibrium modelling was accepted by meteorologists. There is much more to weather modelling than just Lorenz’s complex systems foundation, but his work contributed fundamentally to the dramatic increase in the accuracy of weather forecasts over the last half century—even in the face of global warming that is disturbing the underlying climate which determines the weather.

Likewise, Lorenz’s discovery was considered and applied by all manner of sciences, leading to complexity analysis operating as an important adjunct to the reductionist approach that remains the bedrock of scientific analysis. In 1999, the journal Science recognised this with a special issue devoted to complexity in numerous fields: Physics (Goldenfeld and Kadanoff 1999), Chemistry (Whitesides and Ismagilov 1999), Biology (Parrish and Edelstein-Keshet 1999; Pennisi 1999; Weng, Bhalla, and Iyengar 1999), Evolution (Service 1999), Geography (Werner 1999)—and even Economics (Arthur 1999).

Today, complex systems are an uncontroversial aspect of every science—but not of economics, because the dominant methods in economics are antithetical to the foundations of complexity. These methods include linearity, as Blanchard acknowledged, but more crucially, they involve a perverted form of reductionism that Physics Nobel Laureate Philip Anderson christened “Constructionism”.

1. The impossibility of constructionism with complex systems
   

Anderson’s “More is Different” (Anderson 1972) attacked the idea that, in line with Ernest Rutherford’s quip that “all science is either physics or stamp collecting”, higher-level sciences—like chemistry, biology and even psychology—can and should be reduced to applied physics. Speaking as someone who had made fundamental contributions to particle physics, Anderson asserted that, though “The reductionist hypothesis … among the great majority of active scientists … is accepted without question”, this did not mean that higher-level sciences like chemistry could be generated from what we know about physics. “The main fallacy in this kind of thinking”, he declared:

is that the reductionist hypothesis does not by any means imply a “constructionist” one: The ability to reduce everything to simple fundamental laws does not imply the ability to start from those laws and reconstruct the universe. (Anderson 1972, p. 393. Emphasis added)

The phenomena that made this approach untenable were “the twin difficulties of scale and complexity”, since:

The behavior of large and complex aggregates of elementary particles, it turns out, is not to be understood in terms of a simple extrapolation of the properties of a few particles. Instead, at each level of complexity entirely new properties appear, and the understanding of the new behaviors requires research which I think is as fundamental in its nature as any other…

At each stage entirely new laws, concepts, and generalizations are necessary, requiring inspiration and creativity to just as great a degree as in the previous one. Psychology is not applied biology, nor is biology applied chemistry. (Anderson 1972, p. 393)

And nor is macroeconomics applied microeconomics—but mainstream economists, because of their extreme insularity, haven’t gotten Anderson’s memo. They continue to attempt to do the impossible: to construct the higher-level analysis of macroeconomics via a direct application of the lower-level analysis of microeconomics. That is only possible if all relationships in macroeconomics are linear as Blanchard described them in “Where Danger Lurks” (Blanchard 2014), when the lesson of the Global Financial Crisis was that they obviously are not—and in a subsequent chapter, I will show that there are fundamental nonlinearities in macroeconomics that should be embraced, rather than ignored.

Fittingly, Anderson concluded with two anecdotes from economics:

In closing, I offer two examples from economics of what I hope to have said. Marx said that quantitative differences become qualitative ones, but a dialogue in Paris in the 1920’s sums it up even more clearly:

FITZGERALD: The rich are different from us.

HEMINGWAY: Yes, they have more money. (Anderson 1972, p. 396)

Marx, and money, are two other things that Neoclassical economists ignore. But even more critically, they ignore the logical and empirical fallacies that beset microeconomics. Even if it were possible to derive macroeconomics from microeconomics, Neoclassical microeconomics is not the foundation one should use, because it is manifestly wrong about both consumption and production. Some Neoclassicals are aware of the logical problems with their model of consumption—though their reactions to it are bizarre. But none of them are aware of the empirical fallacies in their model of production.

References

 

Anderson, P. W. 1972. ‘More Is Different: Broken symmetry and the nature of the hierarchical structure of science’, Science, 177: 393-96.

Arthur, W. Brian. 1999. ‘Complexity and the Economy’, Science, 284: 107-09.

Barro, Robert J. 1989. ‘The Ricardian Approach to Budget Deficits’, The Journal of Economic Perspectives, 3: 37-54.

Blanchard, Olivier. 2014. ‘Where Danger Lurks’, Finance & Development, 51.

Goldenfeld, Nigel, and Leo P. Kadanoff. 1999. ‘Simple Lessons from Complexity’, Science, 284: 87-89.

Harrod, R. F. 1939. ‘An Essay in Dynamic Theory’, The Economic Journal, 49: 14-33.

———. 1948. Towards a Dynamic Economics (Macmillan: London).

Hicks, J. R. 1949. ‘Mr. Harrod’s Dynamic Theory’, Economica, 16: 106-21.

Keen, Steve. 1995. ‘Finance and Economic Breakdown: Modeling Minsky’s ‘Financial Instability Hypothesis.”, Journal of Post Keynesian Economics, 17: 607-35.

———. 2020. ‘Burying Samuelson’s Multiplier-Accelerator and resurrecting Goodwin’s Growth Cycle in Minsky.’ in Robert Y. Cavana, Brian C. Dangerfield, Oleg V. Pavlov, Michael J. Radzicki and I. David Wheat (eds.), Feedback Economics : Applications of System Dynamics to Issues in Economics (Springer: New York).

Li, Tien-Yien, and James A. Yorke. 1975. ‘Period Three Implies Chaos’, The American Mathematical Monthly, 82: 985-92.

Lorenz, Edward N. 1963. ‘Deterministic Nonperiodic Flow’, Journal of the Atmospheric Sciences, 20: 130-41.

Mendelsohn, Robert, William D. Nordhaus, and Daigee Shaw. 1994. ‘The Impact of Global Warming on Agriculture: A Ricardian Analysis’, The American Economic Review, 84: 753-71.

Parrish, Julia K., and Leah Edelstein-Keshet. 1999. ‘Complexity, Pattern, and Evolutionary Trade-Offs in Animal Aggregation’, Science, 284: 99-101.

Pennisi, Elizabeth. 1999. ‘Unraveling Bacteria’s Dependable Homing System’, Science, 284: 82-82.

Ricardo, David, and Piero Sraffa. 1952. The works and correspondence of David Ricardo / edited by Piero Sraffa, with the collaboration of M.H. Dobb Vol.6, Letters, 1810-1815 (Cambridge University Press for the Royal Economic Society: Cambridge).

Service, Robert F. 1999. ‘Exploring the Systems of Life’, Science, 284: 80-83.

Weng, Gezhi, Upinder S. Bhalla, and Ravi Iyengar. 1999. ‘Complexity in Biological Signaling Systems’, Science, 284: 92-96.

Werner, B. T. 1999. ‘Complexity in Natural Landform Patterns’, Science, 284: 102-04.

Whitesides, George M., and Rustem F. Ismagilov. 1999. ‘Complexity in Chemistry’, Science, 284: 89-92.