This is the draft of an invited paper for the journal Globalizations on “Economics and the Climate Crisis“. As I’ve argued for some time, Neoclassical economists—especially William Nordhaus and Richard Tol—bear enormous responsibility for trivializing the dangers of climate change on intellectually spurious grounds. This paper is the most comprehensive overview I’ve done of this issue, and it includes new material on Nordhaus’s misreading of scientific literature. Word has deleted the footnotes, which you can find in the attached PDF.
Introduction
William Nordhaus was awarded the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel (Mirowski 2020) in 2018 for his work on climate change. His first major paper in this area was “World Dynamics: Measurement Without Data” (Nordhaus 1973), which attacked the pessimistic predictions in Jay Forrester’s World Dynamics (Forrester 1971; Forrester 1973) on the grounds, amongst others, that they were not firmly grounded in empirical research:
The treatment of empirical relations in World Dynamics can be summarised as measurement without data…Not a single relationship or variable is drawn from caactual data or empirical studies. (Nordhaus 1973, p. 1157. Italics in original. Subsequent emphases added.)
There is no explicit or apparent reference to data or existing empirical studies. (Nordhaus 1973, p. 1182)
Whereas most scientists would require empirical validation of either the assumptions or the predictions of the model before declaring its truth content, Forrester is apparently content with subjective plausibility. (Nordhaus 1973, p. 1183)
Sixth, there is some lack of humility toward predicting the future. Can we treat seriously Forrester’s (or anybody’s) predictions in economics and social science for the next 130 years? Long-run economic forecasts have generally fared quite poorly… And now, without the scantest reference to economic theory or empirical data, Forrester predicts that the world’s material standard of living will peak in 1990 and then decline. (Nordhaus 1973, p. 1183)
After this paper, Nordhaus’s own research focused upon the economics of climate change. One could rightly expect, from his critique of Forrester, that Nordhaus was scrupulous about basing his modelling upon sound empirical data.
One’s expectations would be dashed. Whereas Nordhaus characterised Forrester’s work as “measurement without data”, Nordhaus’s can be characterised as “making up numbers to support a pre-existing belief”: specifically, that climate change could have only a trivial impact upon the economy. This practice was replicated, rather than challenged, by subsequent Neoclassical economists—with some honourable exceptions, notably Weissman (Weitzman 2011; Weitzman 2011), de Canio (DeCanio 2003), Cline (Cline 1996), Darwin (Darwin 1999), Kaufmann (Kaufmann 1997; Kaufmann 1998), and Quiggin and Horowitz (Quiggin and Horowitz 1999).
The end product is a set of purported empirical estimates of the impact of climate change upon the economy that are utterly spurious, and yet which have been used to calibrate the “Integrated Assessment Models” (IAMs) that have largely guided the political responses to climate change. Stephen de Canio expressed both the significance and the danger of this work very well in his neglected book Economic Models of Climate Change: a Critique:
Perhaps the greatest threat from climate change is the risk it poses for large-scale catastrophic disruptions of Earth systems…
Business as usual amounts to conducting a one-time, irreversible experiment of unknown outcome with the habitability of the entire planet.
Given the magnitude of the stakes, it is perhaps surprising that much of the debate about the climate has been cast in terms of economics…
Nevertheless, it is undeniably the case that economic arguments, claims, and calculations have been the dominant influence on the public political debate on climate policy in the United States and around the world… It is an open question whether the economic arguments were the cause or only an ex post justification of the decisions made by both administrations, but there is no doubt that economists have claimed that their calculations should dictate the proper course of action. (DeCanio 2003, pp. 2-4)
The impact of these economists goes beyond merely advising governments, to actually writing the economic components of the formal reports by the IPCC (“Intergovernmental Panel On Climate Change”), the main authority coordinating humanity’s response, such as it is, to climate change. The sanguine conclusions they state—such as the following from the 2014 IPCC Report (Field, Barros et al. 2014)—carry more weight with politicians, obsessed as they are with their countries’ GDP growth rates, than the far more alarming warnings in the sections of the Report written by actual scientists:
Global economic impacts from climate change are difficult to estimate. Economic impact estimates completed over the past 20 years vary in their coverage of subsets of economic sectors and depend on a large number of assumptions, many of which are disputable, and many estimates do not account for catastrophic changes, tipping points, and many other factors. With these recognized limitations, the incomplete estimates of global annual economic losses for additional temperature increases of ~2°C are between 0.2 and 2.0% of income. (Arent, Tol et al. 2014, p. 663. Emphasis added)
This is a prediction, not of a drop in the annual rate of economic growth—which would be significant even, at the lower bound of 0.2%–but a prediction that the level of GDP will be between 0.2% and 2% lower, when global temperatures are 2°C higher than pre-industrial levels, compared to what they would have been in the complete absence of global warming. This involves a trivial decline in the predicted rate of economic growth between 2014 and when the 2°C increase occurs, even at the upper bound of 2%.
Given the impact that economists have had on public policy towards climate change, and the immediacy of the threat we now face from climate change, this work could soon be exposed as the most significant and dangerous hoax in the history of science.
Fictional Empirics
The numerical relationships that economists assert exist between global temperature change and GDP change were summarized in Figure 1 of the chapter “Key Economic Sectors and Services” (Arent, Tol et al. 2014) in the 2014 IPCC Report Climate Change 2014: Impacts, Adaptation, and Vulnerability (Field, Barros et al. 2014). It is reproduced below as Figure 1.
Figure 1: Figure 10.1 from Chapter 10 “Key Economic Sectors and Services” of the IPCC Report Climate Change 2014 Impacts, Adaptation, and Vulnerability
The sources of these numbers—as I explain below, they cannot be called “data points”—are given in Table SM10-1 from the supplement to this report (Arent 2014). Four classifications of the approaches used were listed by the IPCC: “Enumeration” (ten studies); “Statistical” (5 studies); “CGE” (“Computable General Equilibrium”: 2 studies—one with 2 results); and “Expert Elicitation” (1 study).
Enumeration: It’s what you don’t count that counts
The bland description of what the “Enumeration” approach entails given by Tol makes it seem unobjectionable:
In this approach, estimates of the “physical effects” of climate change are obtained one by one from natural science papers, which in turn may be based on some combination of climate models, impact models, and laboratory experiments. The physical impacts must then each be given a price and added up. For agricultural products, an example of a traded good or service, agronomy papers are used to predict the effect of climate on crop yield, and then market prices or economic models are used to value the change in output. (Tol 2009, pp. 31-32)
However, this analysis commenced from the perspective, in the very first reference in this tradition (Nordhaus 1991), that climate change is a relatively trivial issue:
it must be recognised that human societies thrive in a wide variety of climatic zones. For the bulk of economic activity, non-climate variables like labour skills, access to markets, or technology swamp climatic considerations in determining economic efficiency. (Nordhaus 1991, p. 930. Emphasis added)
If there had been a decent evaluation process in place at this time for research into the economic impact of climate change, this paragraph alone should have raised alarm bells: yes, it is quite likely that climate today is a less important determinant of “economic efficiency” today than “labour skills, access to markets, or technology”, when one is comparing one region or country with another today. But what is the relevance of this cross-sectional comparison to assessing the impact of drastically altering the entire planet’s climate over time, via the retention of additional solar energy from additional greenhouse gases?
Nordhaus then excludes 87% of US industry from consideration, on the basis that it takes place “in carefully controlled environments that will not be directly affected by climate change”:
Table 5 shows a sectoral breakdown of United States national income, where the economy is subdivided by the sectoral sensitivity to greenhouse warming. The most sensitive sectors are likely to be those, such as agriculture and forestry, in which output depends in a significant way upon climatic variables. At the other extreme are activities, such as cardiovascular surgery or microprocessor fabrication in ‘clean rooms’, which are undertaken in carefully controlled environments that will not be directly affected by climate change. Our estimate is that approximately 3% of United States national output is produced in highly sensitive sectors, another 10% in moderately sensitive sectors, and about 87% in sectors that are negligibly affected by climate change. (Nordhaus 1991, p. 930. Emphasis added)
The examples of “cardiovascular surgery or microprocessor fabrication in ‘clean rooms'” might seem reasonable activities to describe as taking place in “carefully controlled environments”. However, Nordhaus’s list of industries that he simply assumed would be negligibly impacted by climate change is so broad, and so large, that it is obvious that what he meant by “not be directly affected by climate change” is anything that takes place indoors—or, indeed, underground, since he includes mining as one of the unaffected sectors. Table 1, which is an extract from Nordhaus’s Table 5 (Nordhaus 1991, p. 931), lists the subset of industries that he considered would be “negligibly affected by climate change”.
Table 1: Extract from Nordhaus’s breakdown of economic activity by vulnerability to climatic change in US 1991 $ terms (Nordhaus 1991, p. 931 )
Since this was the first paper in a research tradition, one might hope that subsequent researchers challenged this assumption. However, instead of challenging it, they replicated it. The 2014 IPCC Report repeats the assertion that climate change will be a trivial determinant of future economic performance:
For most economic sectors, the impact of climate change will be small relative to the impacts of other drivers (medium evidence, high agreement). Changes in population, age, income, technology, relative prices, lifestyle, regulation, governance, and many other aspects of socioeconomic development will have an impact on the supply and demand of economic goods and services that is large relative to the impact of climate change. (Arent, Tol et al. 2014, p. 662)
It also repeats the assertion that indoor activities will be unaffected. The one change between Nordhaus in 1991 and the IPCC Report 23 years later is that it no longer lumps mining in the “not really exposed to climate change” bracket. Otherwise it repeats Nordhaus’s assumption that anything done indoors will be unaffected by climate change:
Frequently Asked Questions
FAQ 10.3 | Are other economic sectors vulnerable to climate change too?
Economic activities such as agriculture, forestry, fisheries, and mining are exposed to the weather and thus vulnerable to climate change. Other economic activities, such as manufacturing and services, largely take place in controlled environments and are not really exposed to climate change. (Arent, Tol et al. 2014, p. 688)
All the intervening papers between Nordhaus in 1991 and the IPCC in 2014 maintain this assumption: neither manufacturing, nor mining, transportation, communication, finance, insurance and non-coastal real estate, retail and wholesale trade, nor government services, appear in the “enumerated” industries in the “Coverage” column in Table 3. All these studies have simply assumed that these industries, which account for of the order of 90% of GDP, will be unaffected by climate change.
There is a “poker player’s tell” in FAQ quoted above which implies that these Neoclassical economists are on a par with Donald Trump in their understanding of what climate change really entails. This is the statement that “Economic activities such as agriculture, forestry, fisheries, and mining are exposed to the weather and thus vulnerable to climate change“. Explicitly, they are saying that if an activity is exposed to the weather, it is vulnerable to climate change, but if it is not, it is “not really exposed to climate change”. They are equating the climate to the weather.
This is a harsh judgment to pass on academics, who are supposed to have sufficient intellect to not make such mistakes. But there is no other way to make sense of their collective decision to exclude almost 90% of GDP from their enumeration of damages from climate change. Nor is there any other way to interpret the core assumption of their other dominant method of making up numbers for the models, the so-called “statistical” or “cross-sectional” method.
The “Statistical approach”
While locating the fundamental flaw in the “enumeration” approach took some additional research, the flaw in the statistical approach was obvious in the first reference I read on it, Richard Tol’s much-corrected (Tol 2014) and much-criticised paper (Gelman 2014; Gelman 2015; Nordhaus and Moffat 2017, p. 10; Gelman 2019), “The Economic Effects of Climate Change”:
An alternative approach, exemplified in Mendelsohn’s work (Mendelsohn, Morrison et al. 2000; Mendelsohn, Schlesinger et al. 2000) can be called the statistical approach. It is based on direct estimates of the welfare impacts, using observed variations (across space within a single country) in prices and expenditures to discern the effect of climate. Mendelsohn assumes that the observed variation of economic activity with climate over space holds over time as well; and uses climate models to estimate the future effect of climate change. (Tol 2009, p. 32)
If the methodological fallacy in this reasoning is not immediately apparent—bearing in mind that numerous academic referees have let pass papers making this assumption—think what it would mean if this assumption were correct.
Within the United States, it is generally true that very hot and very cold regions have a lower level of per capita income than median temperature regions. Using the States of the contiguous continental USA for those regions, Florida (average temperature 22.5°C) and North Dakota (average temperature 4.7°C), for example, have lower per capita incomes than New York (average temperature 7.4°C). But the difference in average temperatures is far from the only reason for differences in income, and in the greater scheme of things, the differences are trivial anyway: as American States, at the global level they are all in the high per capita income range (respectively $26,000, $26,700 and $43,300 per annum in 2000 US dollars). A statistical study of the relationship between “Gross State Product” (GSP) per capita and temperature will therefore find a weak, nonlinear relationship, with GSP per capita rising from low temperatures, peaking at medium ones, and falling at higher temperatures.
If you then assume that this same relationship between GDP and temperature will apply as global temperatures rise with Global Warming, you will conclude that Global Warming will have a trivial impact on global GDP. Your conclusion is your assumption.
This is illustrated by Figure 2, which shows a scatter plot of deviations from the national average temperature by State in °C, against the deviations from the national average (GDP per capita) of Gross State Product per capita in percent of GDP (the source data is in Table 4), and a quadratic fit to this data, which has a coefficient of -0.00318, and, as expected, a weak correlation coefficient of 0.31.
Figure 2: Correlation of temperature and USA Gross State Product per capita
This regression thus yields a very poor, but not entirely useless, “in-sample” model of how of temperature deviations from the USA average affect deviations from average US GDP per capita today:
In words, this asserts that Gross State Product per capita falls by 0.318% (of the national average GDP per capita) for every 1°C difference in temperature (from the national average temperature) squared.
An absurd “out of sample” policy recommendation from this model would be that the US’s GDP would increase if hotter and colder States could move towards the average temperature for the USA. This absurd recommendation could be “refined” by using this same data to calculate the optimum temperature for the USA’s GDP, and then proposing that all States move to that temperature. Of course, these “policies” are clearly impossible, simply because the States can’t change their location on the planet.
However, the economists doing these studies reasoned that Global Warming would achieve the same result over time (with the drawback that it would be applied equally to all regions). So they did indeed calculate optimum temperatures for each of the sectors they expected to be affected by climate change—and their calculations excluded the same list of sectors that the “enumeration” approach assumed would be unaffected (manufacturing, mining, services, etc.):
Both the reduced-form and cross-sectional response functions imply that the net productivity of sensitive economic sectors is a hill-shaped function of temperature (Mendelsohn, Schlesinger et al. 2000). Warming creates benefits for countries that are currently on the cool side of the hill and damages for countries on the warm side of the hill. The exact optimum temperature varies by sector. For example, according to the Ricardian model, the optimum temperatures for agriculture, forestry, and energy are 14.2, 14.8 and 8.6°C, respectively. With the reduced form model, the optimum temperatures for agriculture and energy are 11.7 and 10.0. (Mendelsohn, Morrison et al. 2000, p. 558)
They then estimated the impact on GDP of increasing global temperatures, assuming that the same coefficients they found for the relationships between temperature and output today (using what Tol called “the statistical” and Mendelsohn called the “cross-sectional” approach) could be used to estimate the impact of global warming. This resulted in more than one study which concluded that increasing global temperatures via global warming would be beneficial to the economy. Here, for example, is Meldelsohn, Schlesinger et al. on the impact of a 2.5°C increase in global temperatures:
Compared to the size of the economy in 2100 ($217 trillion), the market effects are small… The Cross-sectional climate-response functions imply a narrower range of impacts across GCMs: from $97 to $185 billion of benefits with an average of $145 billion of benefits a year. (Mendelsohn, Schlesinger et al. 2000, p. 41. Italics added)
The, once more, explicit assumption these economists are making is that it doesn’t matter how you alter temperature. Whether this is hypothetically done by altering a region’s location on the planet—which is impossible—or by altering the temperature of the entire planet—which is what Climate Change is going—they assumed that the impact on GDP would be the same.
Expert Opinions—Real and Imagined
Nordhaus conducted the only two surveys of “expert opinions” to estimate the impact of global warming on GDP, in 1994 (Nordhaus 1994), and 2017 (Nordhaus and Moffat 2017). The former asked people from various academic backgrounds to give their estimates of the impact on GDP of three global warming scenarios: (A) a 3°C rise by 2090; (B) a 6°C rise by 2175; and (C) a 6°C rise by 2090. The numbers used by the IPCC from this study in Figure 1 were a 3°C temperature rise for a 3.6% fall in GDP.
Expert opinions are a valid procedure to aggregate knowledge in areas that require a large number of disparate fields to be aggregated, as the climate scientist Tim Lenton and co-authors explained in their paper “Tipping elements in the Earth’s climate system” (Lenton, Held et al. 2008):
formal elicitations of expert beliefs have frequently been used to bring current understanding of model studies, empirical evidence, and theoretical considerations to bear on policy-relevant variables. From a natural science perspective, a general criticism is that expert beliefs carry subjective biases and, moreover, do not add to the body of scientific knowledge unless verified by data or theory. Nonetheless, expert elicitations, based on rigorous protocols from statistics and risk analysis, have proved to be a very valuable source of information in public policymaking. It is increasingly recognized that they can also play a valuable role for informing climate policy decisions. (Lenton, Held et al. 2008, p. 1791)
I cite this paper in contrast to Nordhaus’s here for two reasons: (1) it shows how expert opinion surveys should be conducted; (2) Nordhaus later cites this survey in support of his use of a “damage function” for climate change which lacks tipping points, when this survey explicitly rejects such functions.
Lenton et al.’s survey was sent to 193 scientists, of whom 52 responded. Respondents were specifically instructed to stick to their area of knowledge, rather than to speculate more broadly: “Participants were encouraged to remain in their area of expertise” (Lenton, Held et al. 2008, p. 10). These are listed in Table 2.
Table 2: Fields of expertise for experts surveyed in (Lenton, Held et al. 2008); abridged from Table 1 in (Lenton, Held et al. 2008, p. 10)
Nordhaus’s survey began with a letter requesting 22 people to participate, 18 of whom fully complied, and one partially. Nordhaus describes them as including 10 economists, 4 “other social scientists”, and 5 “natural scientists and engineers”, but also describes eight of the economists as coming from “other subdisciplines of economics (those whose principal concerns lie outside environmental economics)” (Nordhaus 1994, p. 48)—which ipso facto should rule them out from taking part in this expert survey in the first place.
One of them was Larry Summers—who is probably the source of the choicest quotes in the paper, such as “For my answer, the existence value [of species] is irrelevant—I don’t care about ants except for drugs” (Nordhaus 1994, p. 50).
Lenton’s survey combined the expertise of its interviewees in specific fields of climate change to compile a list of large elements of the planet’s climate system (>1,000km in extent) which could be triggered by increases in global temperature of between 0.5°C (disappearance of Arctic summer sea ice) and 6°C (amplified En Nino causing drought in Southeast Asia and elsewhere), on timescales varying from 10 years (Arctic summer sea ice) to 300 years (West Antarctic Ice Shelf disintegration) (Lenton, Held et al. 2008, p. 1788).
Nordhaus’s survey was summarised by a superficially bland pair of numbers—3°C temperature rise and a 3.6% fall in GDP—but that summary hides far more than it reveals. There was extensive disagreement, well documented by Nordhaus, between the relatively tiny cohort of actual scientists surveyed, and in particular the economists “whose principal concerns lie outside environmental economics”. The quotes from the economists surveyed also reveal the source of the predisposition by economists in general to dismiss the significance of climate change.
As Nordhaus noted, “Natural scientists’ estimates [of the damages from climate change] were 20 to 30 times higher than mainstream economists'” (Nordhaus 1994, p. 49). The average estimate by “Non-environmental economists” (Nordhaus 1994, Figure 4, p. 49) of the damages to GDP a 3°C rise by 2090 was 0.4% of GDP; the average for natural scientists was 12.3%, and this was with one of them refusing to answer Nordhaus’s key questions:
Also, although the willingness of the respondents to hazard estimates of subjective probabilities was encouraging, it should be emphasized that most respondents proffered these estimates with reservations and a recognition of the inherent difficulty of the task. One respondent (19), however, was a holdout from such guesswork, writing:
I must tell you that I marvel that economists are willing to make quantitative estimates of economic consequences of climate change where the only measures available are estimates of global surface average increases in temperature. As [one] who has spent his career worrying about the vagaries of the dynamics of the atmosphere, I marvel that they can translate a single global number, an extremely poor surrogate for a description of the climatic conditions, into quantitative estimates of impacts of global economic conditions. (Nordhaus 1994, pp. 50-51)
Comments from economists lay at the other end of the spectrum from this self-absented scientist. Because they had a strong belief in the ability of “human societies” to adapt—born of their acceptance of the Neoclassical model of capitalism, in which “the economy” always returns to equilibrium after a “exogenous shock”—they could not imagine that climate change itself could do significant damage to the economy, whatever it might do to the biosphere itself:
One respondent suggested whimsically that it was hardly surprising, given that the economists know little about the intricate web of natural ecosystems, whereas natural scientists know equally little about the incredible adaptability of human societies…
There is a clear difference in outlook among the respondents, depending on their assumptions about the ability of society to adapt to climatic changes. One was concerned that society’s response to the approaching millennium would be akin to that prevalent during the Dark Ages, whereas another respondent held that the degree of adaptability of human economies is so high that for most of the scenarios the impact of global warming would be “essentially zero”.
An economist explains that in his view energy and brain power are the only limits to growth in the long run, and with sufficient quantities of these it is possible to adapt or develop new technologies so as to prevent any significant economic costs. (Nordhaus 1994, pp. 48-49. All emphases added)
Given this extreme divergence of opinion between economists and scientists, one might imagine that Nordhaus’s next survey would examine the reasons for it. In fact, the opposite applied: his methodology excluded non-economists entirely.
Rather than a survey of experts, this was a literature survey (Nordhaus and Moffat 2017), which ipso facto is another legitimate method to provide data for a topic subject that is difficult to measure, and subject to high uncertainty. He and his co-author searched for relevant articles using the string “”(damage OR impact) AND climate AND cost” (Nordhaus and Moffat 2017, p. 7), which is reasonable, if rather too broad (as they themselves admit in the paper).
The key
flaw in this research was where they looked: they executed their search string in Google, which returned 64 million results, Google Scholar, which returned 2.8 million, and the economics-specific database Econlit, which returned just 1700 studies. On the grounds that there were too many results in Google and Google Scholar, they ignored the results from Google and Google Scholar, and simply surveyed the 1700 articles in Econlit (Nordhaus and Moffat 2017, p. 7). These are, almost exclusively, articles written by economists.
Nordhaus and Moffat read the abstracts of these 1700 to rule out all but 24 papers from consideration. Reading these papers led to just 11 they included in their survey results. The supplemented this “systematic research synthesis (SRS)” with:
a second approach, known as a “non-systematic research summary.” In this approach, the universe of studies was selected by a combination of formal and informal methods, such as the SRS above, the results of the Tol survey, and other studies that were known to the researchers. (Nordhaus and Moffat 2017, p. 8)
Their labours resulted in the addition of just five studies which had not been used either by the IPCC or by Tol in his aggregation papers (Tol 2009; Tol 2018; Tol 2018), with additional 6 results, and 4 additional authors—Cline, Dellink, Kemfert and Hambel—who had not already cited in the empirical estimates literature (though Cline was one of Nordhaus’s interviewees in his 1994 survey).
Remarkably, given that Nordhaus was the lead author of this study, one of the previously unused studies was by Nordhaus himself in 2010 (Nordhaus 2010). (Nordhaus and Moffat 2017)
does not provide details of this paper, or any other paper they uncovered, but I presume it is (Nordhaus 2010), given the date, and the fact that the temperature and damages estimates given in it—a 3.4°C increase in temperature causing a 2.8% fall in GDP—are identical to those given in this paper’s Table 2.
It may seem strange that Nordhaus did not notice that a paper by himself, estimating the damages from climate change, was not included in previous studies. But in fact, there is a good reason for this omission: (Nordhaus 2010) was not an enumerative study, nor a statistical one, let alone the results of an “expert elicitation”, but the output of a run of Nordhaus’s own “Integrated Assessment Model” (IAM), DICE! Treating this as a “data point” is using an output of a model to calibrate the model itself. Nonetheless, these numbers—and the five additional pairs from the four additional studies uncovered by their survey—were added to the list of numbers from which economists like Nordhaus could calibrate what they call their “damage functions”.
Damage Functions
“Damage functions” are the way in which Neoclassical economists connect estimates from scientists of the change in global temperature to their own, as shown in previous sections, utterly unsound estimates of future GDP, given this change in temperature. They reduce GDP from what they claim it would have been in the total absence of climate change, to what they claim it will be, given different levels of temperature rise. The form these damage functions take is normally simply a quadratic:
Nordhaus justifies using a quadratic to describe such an inherently discontinuous as climate change by misrepresenting the scientific literature—specifically, the careful survey of expert opinions carried out by Lenton et al (Lenton, Held et al. 2008) and contrasted earlier to Nordhaus’s survey of largely non-experts (Nordhaus 1994). Nordhaus makes the following statement in his DICE manual, and repeats it in (Nordhaus and Moffat 2017, p. 35):
The current version assumes that damages are a quadratic function of temperature change and does not include sharp thresholds or tipping points, but this is consistent with the survey by Lenton et al. (2008) (Nordhaus and Sztorc 2013, p. 11. Emphasis added)
In The Climate Casino (Nordhaus 2013), Nordhaus states that:
There have been a few systematic surveys of tipping points in earth systems. A particularly interesting one by Lenton and colleagues examined the important tipping elements and assessed their timing… Their review finds no critical tipping elements with a time horizon less than 300 years until global temperatures have increased by at least 3°C. (Nordhaus 2013, p. 60)
These claims can only be described as blatant misrepresentations of “Tipping elements in the Earth’s climate system”(Lenton, Held et al. 2008). The very first element in the summary table of their findings meets two of the three criteria that Nordhaus claimed were not met: Arctic summer sea-ice could be triggered by global warming of between 0.5–2°C, and in a time span measured in decades—see Figure 3.
Figure 3: An extract from Table 1 of “Tipping elements in the Earth’s climate system”,(Lenton, Held et al. 2008, p. 1788)
Nordhaus justifies his omission of Arctic summer sea ice in his table N1 (Nordhaus 2013, p. 333) via a column headed “Level of concern (most concern = ***)”, where it receives the lowest ranking (*)—thus apparently justifying his statement that there was “no critical tipping point” in less than 300 years, and with less than a 3°C temperature increase.
However, no such column exists in Table 1 of Lenton, Held et al. (2008), while their discussion of the ranking of threats puts Arctic summer sea ice first, not last:
We conclude that the greatest (and clearest) threat is to the Arctic with summer sea-ice loss likely to occur long before (and potentially contribute to) GIS melt (Lenton, Held et al. 2008, pp. 1791-92. Emphasis added).
Their treatment of time also differs substantially from that implied by Nordhaus, which is that decisions about tipping elements with time horizons of several centuries can be left for decision makers several centuries hence. While Lenton et al, do give a timeframe of more than 300 years for the complete melting of the Greenland Ice Sheet (GIS), for example, they note that focused on tipping elements whose fate would be decided this century:
Thus, we focus on the consequences of decisions enacted within this century that trigger a qualitative change within this millennium, and we exclude tipping elements whose fate is decided after 2100. (Lenton, Held et al. 2008, p. 1787)
Thus, while the GIS might not melt completely for several centuries, the human actions that will decide whether that happens or not will be taken in this century, not in several hundred years from now.
Finally, the paper’s conclusion began with the warning that smooth functions should not be used, noted that discontinuous climate tipping points were likely to be triggered this century, and reiterated that the greatest threats were Arctic summer sea ice and Greenland:
Conclusion
Society may be lulled into a false sense of security by smooth projections of global change. Our synthesis of present knowledge suggests that a variety of tipping elements could reach their critical point within this century under anthropogenic climate change. The greatest threats are tipping the Arctic sea-ice and the Greenland ice sheet, and at least five other elements could surprise us by exhibiting a nearby tipping point. (Lenton, Held et al. 2008, p. 1792. Emphasis added)
There is thus no empirical or scientific justification for choosing a quadratic to represent damages from climate change—the opposite in fact applies. Regardless, this is the function that Nordhaus ultimately adopted. Given this assumed functional form, the only unknowns are the values of the coefficients a, b and c in Equation .
Ever since Nordhaus started using a quadratic, he has consistently reduced the value of its parameters, from an initial 0.0035 for the quadratic term—which means that global warming is assumed to reduce GDP by 0.35% times the temperature (change over pre-industrial levels) squared—to a final value of 0.00227 (see Equation ). Source documents here are (Nordhaus and Sztorc 2013, pp. 83, 86, 91 & 97 for the 1992, 1999, 2008 and 2013 versions of DICE.; Nordhaus 2017, p. 1 for 2017; Nordhaus 2018, p. 345 for 2018):
This reduction progressively reduced his already trivial predictions of damage to GDP from global warming. For example, his prediction for the impact on GDP of a 4°C increase in temperature—the level he describes as optimal in his “Nobel Prize” lecture, since according to his model, it minimises the joint costs of damage and abatement (Nordhaus 2018, Slides 6 & 7)—was reduced from a 7% fall in 1992 to a 3.6% fall in 2018 (see Figure 4).
Figure 4: How low can you go? Nordhaus’s downward revisions to his damage function
I now turn to doing what Nordhaus himself said a scientist should do, when deriding Forrester’s model—”require empirical validation of either the assumptions or the predictions of the model
before declaring its truth content” (Nordhaus 1973, p. 1183). This is clearly something neither Nordhaus nor other Neoclassical climate change economists did themselves—apart from the honourable mentions noted earlier.
Deconstructing Neoclassical Delusions: GDP and Energy
Nordhaus justified the assumption that 87% of GDP will be unaffected by climate change on the basis that:
for the bulk of the economy—manufacturing, mining, utilities, finance, trade, and most service industries—it is difficult to find major direct impacts of the projected climate changes over the next 50 to 75 years. (Nordhaus 1991, p. 932)
In fact, a direct effect can easily be identified by surmounting the failure of economists in general—not just Neoclassicals—to appreciate the role of energy in production. Almost all economic models use production functions that assume that “Labour” and “Capital” are all that are needed to produce “Output”. However, neither Labour nor Capital can function without energy inputs: “to coin a phrase, labour without energy is a corpse, while capital without energy is a sculpture” (Keen, Ayres et al. 2019, p. 41). Energy is directly needed to produce GDP, and therefore if energy production has to fall because of global warming, then so will GDP.
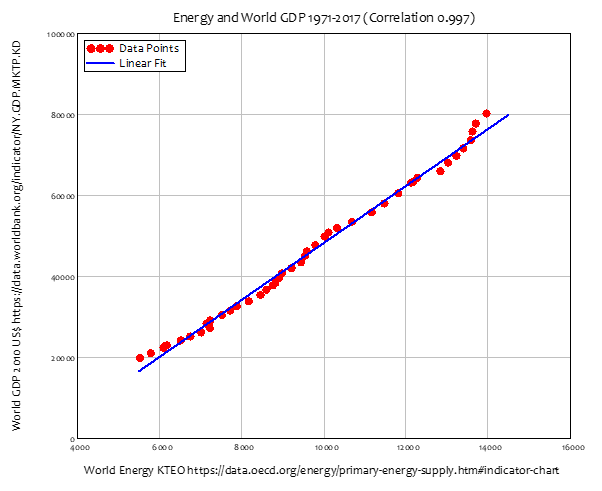
The only question is how much, and the answer, given our dependence on fossil fuels, is a lot. Unlike the trivial correlation between local temperature and local GDP used by Nordhaus and colleagues in the “statistical” method, the correlation between global energy production and global GDP is overwhelmingly strong. A simple linear regression between energy production and GDP has a correlation coefficient of 0.997—see Figure 5.
Figure 5: Energy determines GDP
GDP in turn determines excess CO2 in the atmosphere. A linear regression between GDP and CO2 has a correlation coefficient of 0.998—see Figure 6.
Figure 6: Without significant de-carbonization, GDP determines CO2
Lastly, CO2 very tightly determines the temperature excess over pre-industrial levels. A linear regression between CO2 and the Global Temperature Anomaly has a correlation of 0.992 using smoothed data (which excludes the effect of non-CO2 fluctuations such as the El Nino effect).
Figure 7: CO2 determines Global Warming
Working in reverse, if climatic changes caused by the increase in global temperature persuade the public and policymakers that we must stop adding CO2 to the atmosphere “now”, whenever “now” may be, then global GDP will fall roughly proportionately to the ratio of fossil-fuel energy production to total energy production at that time.
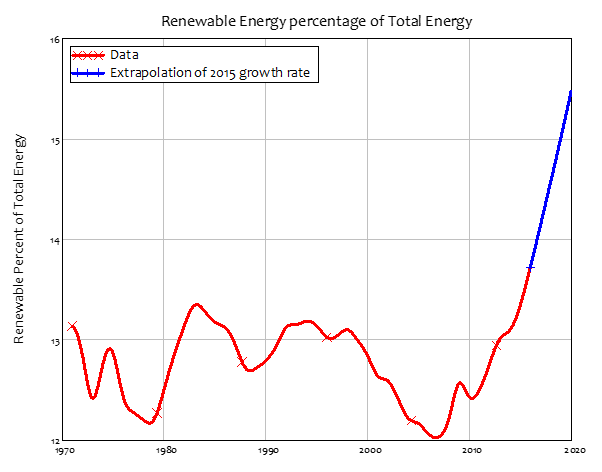
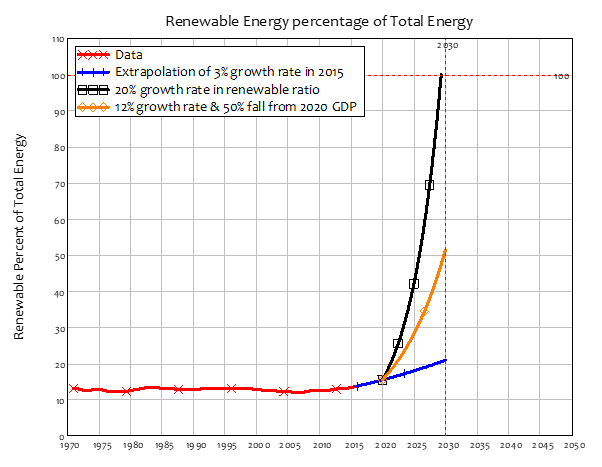
As of 2020, fossil fuels provided roughly 85% of energy production. So, if 2020 were the year humanity decided that the growth in CO2 had to stop, GDP would fall by of the order of 85%. Even if the very high rate of growth of renewables in 2015 were maintained—when the ratio of renewables to total energy production was growing at about 3% per annum—renewables would still yield less than 40% of total energy production in 2050—see Figure 8. This implies a drop in GDP of about 50% at that time. The decision by Neoclassical climate change economists to exclude “manufacturing, mining, utilities, finance, trade, and most service industries” from any consequences from climate change is thus utterly unjustified.
Figure 8: Renewable energy as a percentage of total energy production
Deconstructing Neoclassical Delusions: Statistics
The “cross-sectional approach” of using the coefficients from the geographic temperature:GDP relationship as a proxy for the global temperature:GDP relationship is similarly unjustified. It assumes that it doesn’t matter how one alters temperature: the effect on GDP will be the same. This belief was defended by Tol in an exchange on Twitter between myself, the Climate scientist Daniel Swain, and the Professor of Computational Astrophysics Ken Rice on June 17-18 2019:
Richard Tol: 10K is less than the temperature distance between Alaska and Maryland (about equally rich), or between Iowa and Florida (about equally rich). Climate is not a primary driver of income. https://twitter.com/RichardTol/status/1140591420144869381?s=20
Daniel Swain: A global climate 10 degrees warmer than present is not remotely the same thing as taking the current climate and simply adding 10 degrees everywhere. This is an admittedly widespread misconception, but arguably quite a dangerous one. https://twitter.com/Weather_West/status/1140670647313584129?s=20
Richard Tol: That’s not the point, Daniel. We observe that people thrive in very different climates, and that some thrive and others do not in the same climate. Climate determinism therefore has no empirical support. https://twitter.com/RichardTol/status/1140928458853421057?s=20
Richard Tol: And if a relationship does not hold for climate variations over space, you cannot confidently assert that it holds over time. https://twitter.com/RichardTol/status/1140928893878263808?s=20
Steve Keen: The cause of variations over space is utterly different to that over time. That they are comparable is the most ridiculous and dangerous “simplifying assumption” in the history of economics. https://twitter.com/ProfSteveKeen/status/1140941982082244608?s=20
Ken Rice: Can I just clarify. Are you actually suggesting that a 10K rise in global average surface temperature would be manageable? https://twitter.com/theresphysics/status/1140661721633308673?s=20
Richard Tol: We’d move indoors, much like the Saudis have. https://twitter.com/RichardTol/status/1140669525081415680?s=20
As with the decision to exclude ~90% of GDP from damages from climate change, Tol’s assumed equivalence of weather changes across space with climate change over time ignores the role of energy in causing climate change. This can be illustrated by annotating his third tweet above with respect to the amount of energy needed to bring about a 10°C temperature increase for the atmosphere:
And if a relationship does not hold for climate variations over space [without changing the energy level of the atmosphere], you cannot confidently assert that it holds over time [as the Solar energy retained in the atmosphere rises by more than 50,000 million Terajoules]. (Trenberth 1981)
To put this level of energy in more comprehensible terms, this is the equivalent of 860 million Hiroshima atomic bombs. That amount of additional energy in the atmosphere would lead to sustained “wet bulb” temperatures that would be fatal for humans in the Tropics and much of the sub-tropics (Raymond, Matthews et al. 2020; Xu, Kohler et al. 2020). A 10°C temperature increase is of the order of that which caused the end-Permian extinction event, the most extreme mass-extinction in Earth’s history (Penn, Deutsch et al. 2018). It is five times the level of global temperature increase that climate scientists fear could trigger “tripping cascades” could transform the planet into a “Hothouse Earth” (Steffen, Rockström et al. 2018; Lenton, Rockström et al. 2019), which could potentially be incompatible with human existence:
Hothouse Earth is likely to be uncontrollable and dangerous to many, particularly if we transition into it in only a century or two, and it poses severe risks for health, economies, political stability (especially for the most climate vulnerable), and ultimately, the habitability of the planet for humans. (Steffen, Rockström et al. 2018, p. 8256)
It therefore very much does matter how one alters the temperature. At the planetary level, there are 3 main determinants of the temperature at any point on the globe:
- Variations in the solar energy reaching the Earth;
- Variations in the amount of this energy retained by greenhouse gases; and
- Differences in location on the planet—primarily differences in distance from the Equator
What the “cross-sectional method” did was derive parameters for the third factor, and then simply assume that the same parameters applied to the second. This is comparable to carefully measuring the terrain of a mountain in the North-South direction, and then using that information to advise on the safety of traversing it East to West.
Econometrics before Ecology
This weakness of the “cross-sectional approach” has been admitted in a more recent paper in this tradition:
Firstly, the literature relies primarily on the cross-sectional approach (see, for instance, Sachs and Warner 1997, Gallup et al. 1999, Nordhaus 2006, and Dell et al. 2009), and as such does not take into account the time dimension of the data (i.e., assumes that the observed relationship across countries holds over time as well). (Kahn, Mohaddes et al. 2019, p. 2. Emphasis added)
This promising start was unfortunately neutered by their eventual simple linear extrapolation of the change in the relationship temperature to GDP relationship between 1960 and 2014 forward to 2100:
We start by documenting that the global average temperature has risen by 0:0181 degrees Celsius per year over the last half century… We show that an increase in average global temperature of 0:04°C per year— corresponding to the Representative Concentration Pathway (RCP) 8.5 scenario (see Figure 1), which assumes higher greenhouse gas emissions in the absence of mitigation policies— reduces world’s real GDP per capita by 7.22 percent by 2100. (Kahn, Mohaddes et al. 2019, p. 4)
Their predictions for GDP change as a function of temperature change is the shaded region in Figure 9 (which reproduces their Figure 2). The linearity of their projection is evident: it presumes no structural change in the relationship between global temperature and GDP, even as temperature rises by 3.2°C over their time horizon of 80 years (0.04°C per year from 2020 till 2100).
Figure 9: Kahn and Mohaddes’s linear extrapolation of the temperature:GDP relationship from 1960-2014 out till 2100 (Kahn, Mohaddes et al. 2019, p. 6)
The failure of this paper to account for the obvious discontinuities such a temperature increase will wreak on the planet’s climate was acknowledged by one of the authors on Twitter on October 31st 2019:
Kamiar Mohaddes: I also want to be clear that we cannot, and do not, claim that our empirical analysis allows for rare disaster events, whether technological or climatic, which is likely to be an important consideration. From this perspective, the counterfactual outcomes that we discuss… in Section 4 of the paper (see: https://ideas.repec.org/p/cam/camdae/1965.html) should be regarded as conservative because they only consider scenarios where the climate shocks are Gaussian, without allowing for rare disasters. https://twitter.com/KamiarMohaddes/status/1189846383307694084?s=20 ; https://twitter.com/KamiarMohaddes/status/1189846648366796800?s=20
Steve Keen: Kamiar, the whole point of #GlobalWarming is that it shifts the entire distribution. What is “rare” in our current climate—like for example the melting of Greenland—becomes a certainty at higher temperatures. https://twitter.com/ProfSteveKeen/status/1189849936290029569?s=20
What Mohaddes called “rare disaster events”—such as, for example, the complete disappearance of the Arctic Ice sheet during summer—would indeed be rare at our current global temperature. But they become certainties as the temperature rises another 3°C (Steffen, Rockström et al. 2018, Figure 3, p. 8255). This forecast is as useful as a study of the relationship between temperature and speed skating, which concludes that it would be advantageous to increase the temperature of the ice from -2°C to +2°C.
This recent paper alerted me to one potentially promising study I had previously missed: the significant outlier in Figure 9 by Burke et al. (Burke, Hsiang et al. 2015). This was at least outside the economic ballpark, if not in that of scientists like Steffen, who expect a 4°C increase in temperature to lead to the collapse of civilisation (Moses 2020).
As its title “Global non-linear effect of temperature on economic production” implies, it did at least consider nonlinearities in the Earth’s climate. But once again, this was restricted to nonlinearities in the relationship between 1960 and 2010, and it was then extrapolated to a future planet with a vastly different climate:
We quantify the potential impact of warming on national and global incomes by combining our estimated non-linear response function with ‘business as usual’ scenarios of future warming and different assumptions regarding future baseline economic and population growth. This approach assumes future economies respond to temperature changes similarly to today’s economies—perhaps a reasonable assumption given the observed lack of adaptation during our 50-year sample… climate change reduces projected global output by 23% in 2100 relative to a world without climate change, although statistical uncertainty allows for positive impacts with probability 0.29 (Burke, Hsiang et al. 2015, pp. 237-38. Emphasis added)
As applies to so much of this research, these two recent papers show the authors delighting in the ecstasy of econometrics, while failing to appreciate the irrelevance of their framework to the question at hand.
GIGO: Garbage In, Garbage Out
When I began this research, I expected that the main cause of Nordhaus’s extremely low predictions of damages from climate change would be the application of a very high discount rate to climate damages estimated by scientists, and that a full critique of his work would require explaining why an equilibrium-based Neoclassical model like DICE was the wrong tool to analyse something as dynamic and far from equilibrium as climate change (DeCanio 2003). Instead, I found that the computing adage “Garbage In, Garbage Out” (GIGO) applied: it does not matter how good or how bad the actual model is, when it is fed “data” like that concocted by Nordhaus and his coterie of like-minded Neoclassical economists. The numerical estimates to which they fitted their inappropriate models are, as shown here, utterly unrelated to the phenomenon of global warming. Even an appropriate model of the relationship between climate change and GDP would return garbage predictions if it were trained on “data” like this.
This raises the key question: how did such transparently inadequate work get past academic referees?
Simplifying Assumptions and the Refereeing Process: the Poachers becomes the Gatekeepers
One undeniable reason why this research agenda was not drowned at birth was the proclivity for Neoclassical economists to make assumptions on which their conclusions depend, and then dismiss any objections to them on the grounds that they are merely “simplifying assumptions”.
As Paul Romer observed, the standard justification for this is “Milton Friedman’s (1953) methodological assertion from unnamed authority that “the more significant the theory, the more unrealistic the assumptions” (Romer 2016, p. 5). Those who make this defence do not seem to have noted Friedman’s footnote that “The converse of the proposition does not of course hold: assumptions that are unrealistic (in this sense) do not guarantee a significant theory” (Friedman 1953, p. 14).
A simplifying assumption is something which, if it is violated, makes only a small difference to your analysis. Musgrave points out that “Galileo’s assumption that air-resistance was negligible for the phenomena he investigated was a true statement about reality, and an important part of the explanation Galileo gave of those phenomena” (Musgrave 1990, p. 380). However, the kind of assumptions that Neoclassical economists frequently make, are ones where if the assumption is false, then the theory itself is invalidated (Keen 2011, pp. 158-174).
This is clearly the case here with the core assumptions of Nordhaus and his Neoclassical colleagues. If activities that occur indoors are, in fact, subject to climate change; if the temperature to GDP relationships across space cannot be used as proxies for the impact of global warming on GDP, then their conclusions are completely false. Climate change will be at least one order of magnitude more damaging to the economy than their numbers imply—working solely from the spurious assumption that 90% of the economy will be unaffected by it. It could be far, far worse.
Unfortunately, referees who accept Friedman’s dictum that “a theory cannot be tested by the “realism” of its “assumptions”” (Friedman 1953, p. 23) are unlikely to reject a paper because of its assumptions, especially if that paper otherwise makes assumptions that Neoclassical economists accept. Thus, Nordhaus’s initial sorties in this area received a free pass.
After this, a weakness of the refereeing process took over. As any published academic knows, once you are published in an area, you will be selected by journal editors as a referee for that area. Thus, rather than peer review providing an independent check on the veracity of research, it can allow the enforcement of a hegemony. As one of the first of the very few Neoclassical economists to work on climate change, and the first to proffer empirical estimates of the damages to the economy from climate change, this put Nordhaus in the position to both frame the debate, and to play the role of gatekeeper. One can surmise that he relishes this role, given not only his attacks on Forrester and the Limits to Growth (Meadows, Randers et al. 1972; Nordhaus 1973; Nordhaus 1992), but also his attack on his fellow Neoclassical economist Nicholas Stern for using a low discount rate in The Stern Review (Nordhaus 2007; Stern 2007).
The product has been a degree of conformity in this community that even Tol acknowledged:
it is quite possible that the estimates are not independent, as there are only a relatively small number of studies, based on similar data, by authors who know each other well… although the number of researchers who published marginal damage cost estimates is larger than the number of researchers who published total impact estimates, it is still a reasonably small and close-knit community
who may be subject to group-think, peer pressure, and self-censoring. (Tol 2009, pp. 37, 42-43)
Indeed.
Conclusion: Drastically underestimating damages from Global Warming
Were climate change an effectively trivial area of public policy, then the appallingly bad work done by Neoclassical economists on climate change would not matter greatly. It could be treated, like the intentional Sokal hoax (Sokal 2008), as merely a salutary tale about the foibles of the Academy.
But the impact of climate change upon the economy, human society, and the viability of the Earth’s biosphere in general, are matters of the greatest importance. That work this bad has been done, and been taken seriously, is therefore not merely an intellectual travesty like the Sokal hoax. If climate change does lead to the catastrophic outcomes that some scientists now openly contemplate (Kulp and Strauss 2019; Lenton, Rockström et al. 2019; Wang, Jiang et al. 2019; Yumashev, Hope et al. 2019; Lynas 2020; Moses 2020; Raymond, Matthews et al. 2020; Xu, Kohler et al. 2020), then these Neoclassical economists will be complicit in causing the greatest crisis, not merely in the history of capitalism, but potentially in the history of life on Earth.
Appendix
Table 3: Table SM10-1, p. SM10-4 of “Key Economic Sectors, plus other studies by economists
Table 4: USA average temperature, GDP/GSP and Population data
References
Arent, D. J., R.S.J. Tol, E. Faust, J.P. Hella, S. Kumar, K.M. Strzepek, F.L. Tóth, and D. Yan, (2014). Key economic sectors and services – supplementary material. . Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. C. B. Field, V. R. Barros, D. J. Dokkenet al.
Arent, D. J., R. S. J. Tol, et al. (2014). Key economic sectors and services. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. C. B. Field, V. R. Barros, D. J. Dokkenet al. Cambridge, United Kingdom, Cambridge University Press: 659-708.
Bosello, F., F. Eboli, et al. (2012). “Assessing the economic impacts of climate change.” Review of Energy Environment and Economics
1(9).
Burke, M., S. M. Hsiang, et al. (2015). “Global non-linear effect of temperature on economic production.” Nature
527(7577): 235.
Cline, W. (1996). “The impact of global warming on agriculture: Comment.” The American Economic Review
86(5): 1309-1311.
Darwin, R. (1999). “The Impact of Global Warming on Agriculture: A Ricardian Analysis: Comment.” American Economic Review
89(4): 1049-1052.
DeCanio, S. J. (2003). Economic models of climate change : a critique. New York, Palgrave Macmillan.
Fankhauser, S. (1995). Valuing Climate Change: The economics of the greenhouse. London, Earthscan.
Field, C. B., V. R. Barros, et al. (2014). IPCC, 2014: Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom, Cambridge University Press, .
Forrester, J. W. (1971). World Dynamics. Cambridge, MA, Wright-Allen Press.
Forrester, J. W. (1973). World Dynamics. Cambridge, MA, Wright-Allen Press.
Friedman, M. (1953). The Methodology of Positive Economics. Essays in positive economics. Chicago, University of Chicago Press: 3-43.
Gelman, A. (2014). “A whole fleet of gremlins: Looking more carefully at Richard Tol’s twice-corrected paper, “The Economic Effects of Climate Change”.” Statistical Modeling, Causal Inference, and Social Science https://statmodeling.stat.columbia.edu/2014/05/27/whole-fleet-gremlins-looking-carefully-richard-tols-twice-corrected-paper-economic-effects-climate-change/.
Gelman, A. (2015). “More gremlins: “Instead, he simply pretended the other two estimates did not exist. That is inexcusable.”.” Statistical Modeling, Causal Inference, and Social Science https://statmodeling.stat.columbia.edu/2015/07/23/instead-he-simply-pretended-the-other-two-estimates-did-not-exist-that-is-inexcusable/.
Gelman, A. (2019). “The climate economics echo chamber: Gremlins and the people (including a Nobel prize winner) who support them.” https://statmodeling.stat.columbia.edu/2019/11/01/the-environmental-economics-echo-chamber-gremlins-and-the-people-including-a-nobel-prize-winner-who-support-them/.
Hope, C. (2006). “The marginal impact of CO2 from PAGE2002: an integrated assessment model incorporating the IPCC’s five Reasons for Concern.” Integrated Assessment
6(1): 19-56.
Kahn, M. E., K. Mohaddes, et al. (2019) “Long-Term Macroeconomic Effects of Climate Change: A Cross-Country Analysis.” DOI: https://doi.org/10.24149/gwp365.
Kaufmann, R. K. (1997). “Assessing The Dice Model: Uncertainty Associated With The Emission And Retention Of Greenhouse Gases.” Climatic Change
35(4): 435-448.
Kaufmann, R. K. (1998). “The impact of climate change on US agriculture: a response to Mendelssohn et al. (1994).” Ecological Economics
26(2): 113-119.
Keen, S. (2011). Debunking economics: The naked emperor dethroned? London, Zed Books.
Keen, S., R. U. Ayres, et al. (2019). “A Note on the Role of Energy in Production.” Ecological Economics
157: 40-46.
Kulp, S. A. and B. H. Strauss (2019). “New elevation data triple estimates of global vulnerability to sea-level rise and coastal flooding.” Nature Communications
10(1): 4844.
Lenton, T., J. Rockström, et al. (2019). “Climate tipping points – too risky to bet against.” Nature
575(7784): 592-595.
Lenton, T. M., H. Held, et al. (2008). “Supplement to Tipping elements in the Earth’s climate system.” Proceedings of the National Academy of Sciences
105(6).
Lenton, T. M., H. Held, et al. (2008). “Tipping elements in the Earth’s climate system.” Proceedings of the National Academy of Sciences
105(6): 1786-1793.
Lynas, M. (2020). Our Final Warning: Six Degrees of Climate Emergency. London, HarperCollins Publishers.
Maddison, D. (2003). “The amenity value of the climate: the household production function approach.” Resource and Energy Economics
25(2): 155-175.
Maddison, D. and K. Rehdanz (2011). “The impact of climate on life satisfaction.” Ecological Economics
70(12): 2437-2445.
Meadows, D. H., J. Randers, et al. (1972). The limits to growth. New York, Signet.
Mendelsohn, R., W. Morrison, et al. (2000). “Country-Specific Market Impacts of Climate Change.” Climatic Change
45(3): 553-569.
Mendelsohn, R., M. Schlesinger, et al. (2000). “Comparing impacts across climate models.” Integrated Assessment
1(1): 37-48.
Mirowski, P. (2020). The Neoliberal Ersatz Nobel Prize. Nine Lives of Neoliberalism. D. Plehwe, Q. Slobodian and P. Mirowski. London, Verso: 219-254.
Moses, A. (2020). ‘Collapse of civilisation is the most likely outcome’: top climate scientists. Voice of Action. Melbourne, Australia.
Musgrave, A. (1990). ‘Unreal Assumptions’ in Economic Theory: The F-Twist Untwisted. Milton Friedman: Critical assessments. Volume 3. J. C. Wood and R. N. Woods. London and New York, Routledge: 333-342.
Nordhaus, W. (1994). “Expert Opinion on Climate Change.” American Scientist
82(1): 45–51.
Nordhaus, W. (2007). “Critical Assumptions in the Stern Review on Climate Change.” Science
317(5835): 201-202.
Nordhaus, W. (2008). A Question of Balance. New Haven, CT, Yale University Press.
Nordhaus, W. (2013). The Climate Casino: Risk, Uncertainty, and Economics for a Warming World. New Haven, CT, Yale University Press.
Nordhaus, W. (2018). “Nobel Lecture in Economic Sciences. Climate Change: The Ultimate Challenge for Economics.” from https://www.nobelprize.org/uploads/2018/10/nordhaus-slides.pdf.
Nordhaus, W. (2018). “Projections and Uncertainties about Climate Change in an Era of Minimal Climate Policies.” American Economic Journal: Economic Policy
10(3): 333–360.
Nordhaus, W. and J. G. Boyer (2000). Warming the World: Economic Models of Global Warming. Cambridge, Massachusetts, MIT Press.
Nordhaus, W. and P. Sztorc (2013). DICE 2013R: Introduction and User’s Manual.
Nordhaus, W. D. (1973). “World Dynamics: Measurement Without Data.” The Economic Journal
83(332): 1156-1183.
Nordhaus, W. D. (1991). “To Slow or Not to Slow: The Economics of The Greenhouse Effect.” The Economic Journal
101(407): 920-937.
Nordhaus, W. D. (1992). “Lethal Model 2: The Limits to Growth Revisited.” Brookings Papers on Economic Activity(2): 1-43.
Nordhaus, W. D. (1994). “Expert Opinion on Climatic Change.” American Scientist
82(1): 45-51.
Nordhaus, W. D. (1994). Managing the global commons : the economics of climate change / William D. Nordhaus. Cambridge, Mass., Cambridge, Mass.
Nordhaus, W. D. (2006). “Geography and macroeconomics: New data and new findings.” Proceedings of the National Academy of Sciences of the United States of America
103(10): 3510-3517.
Nordhaus, W. D. (2010). “Economic aspects of global warming in a post-Copenhagen environment.” Proceedings of the National Academy of Sciences of the United States of America
107(26): 11721-11726.
Nordhaus, W. D. (2017). “Revisiting the social cost of carbon Supporting Information.” Proceedings of the National Academy of Sciences
114(7): 1-2.
Nordhaus, W. D. and A. Moffat (2017). A Survey Of Global Impacts Of Climate Change: Replication, Survey Methods, And A Statistical Analysis. New Haven, Connecticut, Cowles Foundation. Discussion Paper No. 2096.
Nordhaus, W. D. and Z. Yang (1996). “A Regional Dynamic General-Equilibrium Model of Alternative Climate-Change Strategies.” The American Economic Review
86(4): 741-765.
Penn, J. L., C. Deutsch, et al. (2018). “Temperature-dependent hypoxia explains biogeography and severity of end-Permian marine mass extinction.” Science
362(6419): eaat1327.
Plambeck, E. L. and C. Hope (1996). “PAGE95: An updated valuation of the impacts of global warming.” Energy Policy
24(9): 783-793.
Quiggin, J. and J. Horowitz (1999). “The impact of global warming on agriculture: A Ricardian analysis: Comment.” The American Economic Review
89(4): 1044-1045.
Raymond, C., T. Matthews, et al. (2020). “The emergence of heat and humidity too severe for human tolerance.” Science Advances
6(19): eaaw1838.
Rehdanz, K. and D. Maddison (2005). “Climate and happiness.” Ecological Economics
52(1): 111-125.
Romer, P. (2016). “The Trouble with Macroeconomics.” https://paulromer.net/trouble-with-macroeconomics-update/WP-Trouble.pdf.
Roson, R. and D. v. d. Mensbrugghe (2012). “Climate change and economic growth: impacts and interactions.” International Journal of Sustainable Economy
4(3): 270-285.
Sokal, A. D. (2008). Beyond the hoax : science, philosophy and culture / Alan Sokal. Oxford, Oxford : Oxford University Press.
Steffen, W., J. Rockström, et al. (2018). “Trajectories of the Earth System in the Anthropocene.” Proceedings of the National Academy of Sciences
115(33): 8252-8259.
Stern, N. (2007). The Economics of Climate Change: The Stern Review. Cambridge, Cambridge University Press.
Tol, R. S. J. (1995). “The damage costs of climate change toward more comprehensive calculations.” Environmental and Resource Economics
5(4): 353-374.
Tol, R. S. J. (2002). “Estimates of the Damage Costs of Climate Change. Part 1: Benchmark Estimates.” Environmental and Resource Economics
21(1): 47-73.
Tol, R. S. J. (2009). “The Economic Effects of Climate Change.” The Journal of Economic Perspectives
23(2): 29–51.
Tol, R. S. J. (2014). “Correction and Update: The Economic Effects of Climate Change.” The Journal of Economic Perspectives
28(2): 221-226.
Tol, R. S. J. (2018). “The Economic Impacts of Climate Change.” Review of Environmental Economics and Policy
12(1): 4-25.
Tol, R. S. J. (2018). “The Economic Impacts of Climate Change Appendix.” Review of Environmental Economics and Policy
12(1): 4-25.
Trenberth, K. E. (1981). “Seasonal variations in global sea level pressure and the total mass of the atmosphere.” Journal of Geophysical Research: Oceans
86(C6): 5238-5246.
Wang, X. X., D. Jiang, et al. (2019). “Extreme temperature and precipitation changes associated with four degree of global warming above pre-industrial levels.” International Journal Of Climatology
39(4): 1822-1838.
Weitzman, M. L. (2011). “Fat-Tailed Uncertainty in the Economics of Catastrophic Climate Change.” Review of Environmental Economics and Policy
5(2): 275-292.
Weitzman, M. L. (2011). “Revisiting Fat-Tailed Uncertainty in the Economics of Climate Change.” REEP Symposium on Fat Tails
5(2).
Xu, C., T. A. Kohler, et al. (2020). “Future of the human climate niche.” Proceedings of the National Academy of Sciences: 201910114.
Yumashev, D., C. Hope, et al. (2019). “Climate policy implications of nonlinear decline of Arctic land permafrost and other cryosphere elements.” Nature Communications
10(1): 1900.
and desired investment 
. There is no economic theory, Keynesian or otherwise, that says that this addition makes any sense (
(with ):
. This residual role for the wages-share of output manifests itself in the model dynamics as well: before the crisis, the wages share falls as the debt level rises, while the profit share fluctuates around its equilibrium. This confirms Marx’s intuition in Capital I that wages are a dependent variable in capitalism: “To put it mathematically: the rate of accumulation is the independent, not the dependent, variable; the rate of wages, the dependent, not the independent, variable” (
”
, so that:
(ignoring for simplicity), we get
