Abstract

Though Minsky developed a compelling verbal model of the “Financial Instability Hypothesis” (FIH), he abandoned his early attempts to build a mathematical model of financial instability (Minsky 1957). While many mathematical models of the FIH have been developed since, the criticism that these models are “ad hoc” lingers.

In this paper I show that the essential characteristics of Minsky’s hypothesis are emergent properties of a complex systems macroeconomic model which is derived directly from macroeconomic definitions, augmented by the simplest possible assumptions for relations between system states, and the simplest possible behavioural postulates.

I also show that credit, which I define as the time derivative of private debt, is an essential component of aggregate demand and aggregate income, given that bank lending creates money (Holmes 1969; Moore 1979; McLeay, Radia et al. 2014).

Minsky’s Financial Instability Hypothesis is thus derived from sound macrofoundations. This stylized complex-systems model reproduces not only the core predictions of Minsky’s verbal hypothesis, but also empirical properties of the real world which have defied Neoclassical understanding, and which were also not predictions of Minsky’s verbal model: the occurrence of a “Great Moderation”—a period of diminishing cycles in employment, inflation, and economic growth—prior to a “Minsky Moment” crisis; and a tendency for inequality to rise over time.

The simulations in this paper use the Open Source system dynamics program Minsky, which was named in Minsky’s honour.

Keywords

Minsky, Financial Instability Hypothesis, Complexity, System Dynamics, Credit, Debt, Macroeconomics

JEL Codes

C60, C61, C62, E11, E12, E31, E40, E44, F47, G01, G12, G51, N11, N12, Y1,

Introduction

Though Minsky developed a compelling verbal model of the “Financial Instability Hypothesis” (FIH), he abandoned his early attempts to build a mathematical model of financial instability (Minsky 1957). Many mathematical models of the FIH have been developed since (Taylor and O’Connell 1985; Jarsulic 1989; Keen 1995; Charles 2005; Cruz 2005; Tymoigne 2006; Charles 2008; Fazzari, Ferri et al. 2008; Santos and Macedo e Silva 2009), and Minsky collaborated in some of them (Gatti, Delli Gatti et al. 1994), but the criticism that these models are “ad hoc” lingers (Rosser 1999, p. 83).

In this paper I show that the essential characteristics of Minsky’s hypothesis are emergent properties of a complex systems macroeconomic model which is derived directly from macroeconomic definitions, augmented by the simplest possible assumptions for relations between system states, and the simplest possible behavioural postulates.

I also show that credit—which I define as the time derivative of private debt (see Appendix A)—is an essential component of aggregate demand and aggregate income, given that bank lending creates money (Holmes 1969; Moore 1979; McLeay, Radia et al. 2014).

Minsky’s Financial Instability Hypothesis is thus derived from sound macrofoundations. This stylized complex-systems model reproduces not only the core predictions of Minsky’s verbal hypothesis, but also empirical properties of the real world which have defied Neoclassical understanding, and which were also not predictions of Minsky’s verbal model: the occurrence of a “Great Moderation”—a period of diminishing cycles in employment, inflation, and economic growth—prior to a “Minsky Moment” crisis; and a tendency for inequality to rise over time (Piketty 2014).

Deriving Minsky directly from macroeconomic definitions

Minsky’s Financial Instability Hypothesis is one of the rarest things in the history of economics: a powerful and accurate intuition. Neoclassical economists from Jevons onward have portrayed capitalism as a system that tends to equilibrium—while ignoring both history, and mathematical results like the Perron-Frobenius theorem (Jorgenson 1960; Jorgenson 1961; Jorgenson 1963; McManus 1963; Blatt 1983, , pp. 111-146), that establish otherwise. Marxists predict a perpetual tendency towards stagnation, via simplistic applications of Marx’s “tendency for the rate of profit to fall” (Marx 1894, Chapter 13), or its obverse that “that surplus must have a strong and persistent tendency to rise” (Baran 1968, p. 67). Starting from the still-disputed proposition—not just in Neoclassical economics (Bernanke 2000, p. 24), but in Post Keynesian economics as well (Fiebiger 2014; Keen 2014; Lavoie 2014; Palley 2014; Keen 2015)—that there was a “relation between debt and income” (Minsky 1982, p, 66), Minsky instead deduced that “the fundamental instability of a capitalist economy is upward”. Given the proclivity of economists to model an economist’s theory without having understood it (Hicks 1937; Hicks 1981), this pivotal passage is worth quoting at length:

The natural starting place for analyzing the relation between debt and income is to take an economy with a cyclical past that is now doing well. The inherited debt reflects the history of the economy, which includes a period in the not too distant past in which the economy did not do well… As the period over which the economy does well lengthens, two things become evident in board rooms. Existing debts are easily validated and units that were heavily in debt prospered; it paid to lever. After the event it becomes apparent that the margins of safety built into debt structures were too great. As a result, over a period in which the economy does well, views about acceptable debt structure change. In the deal-making that goes on between banks, investment bankers, and businessmen, the acceptable amount of debt to use in financing various types of activity and positions increases. This increase in the weight of debt financing raises the market price of capital assets and increases investment. As this continues the economy is transformed into a boom economy.

Stable growth is inconsistent with the manner in which investment is determined in an economy in which debt-financed ownership of capital assets exists, and the extent to which such debt financing can be carried is market determined. It follows that the fundamental instability of a capitalist economy is upward. The tendency to transform doing well into a speculative investment boom is the basic instability in a capitalist economy. (Minsky 1982, p, 66. Emphasis added)

Minsky explained the source of his “preanalytic cognitive act … called Vision” (Schumpeter 1954, p. 41) that led to the Financial Instability Hypothesis as his desire to explain what causes Great Depressions:

Can “It”—a Great Depression—happen again? And if “It” can happen, why didn’t “It” occur in the years since World War II? These are questions that naturally follow from both the historical record and the comparative success of the past thirty-five years. To answer these questions it is necessary to have an economic theory which makes great depressions one of the possible states in which our type of capitalist economy can find itself. (Minsky 1982, p. xix. Emphasis added)

Though this was a compelling and ultimately successful Vision, the dominant Vision in macroeconomics remains the need to derive it from “good” foundations, where Neoclassical economists have defined “good” as the capacity to derive macroeconomics from microeconomics. As Robert Lucas, the father of “rational expectations macroeconomics”, put it in an address subtitled “My Keynesian Education”:

I also held on to Patinkin’s ambition somehow, that the theory ought to be microeconomically founded, unified with price theory. I think this was a very common view… Nobody was satisfied with IS-LM as the end of macroeconomic theorizing. The idea was we were going to tie it together with microeconomics and that was the job of our generation. Or to continue doing that. That wasn’t an anti-Keynesian view. (Lucas 2004, p. 20)

Despite the failure of the models derived from this Vision to anticipate the Great Recession, this remains the core Vision in economics. Even the relatively progressive mainstream economist Olivier Blanchard could see no alternative to deriving macroeconomics from microeconomics:

Starting from explicit microfoundations is clearly essential; where else to start from? (Blanchard 2018, p. 47)

The answer to Blanchard’s question is surprisingly simple: you can start directly from macroeconomics itself. The fundamentals of Minsky’s successful hypothesis can be derived directly from incontestable macroeconomic definitions, allied to the simplest possible definitions for both key economic relationships and essential behavioural functions.

The essential macroeconomic definitions needed are the employment rate , the wages share of GDP , the private debt to GDP ratio , the output to employment ratio , and the capital to output ratio :

         

When the first three of these are differentiated with respect to time, three true-by-definition dynamic statements result:

• The employment rate will rise if economic growth exceeds the sum of change in the output to labour ratio and population growth;
• The wages share of output will rise if the total wages grow faster than GDP; and
• The private debt to GDP ratio will rise if private debt growth exceeds the rate of economic growth

These statements are shown in Equation , where is used to signify :

         

The following simplifying assumptions are used to turn these definitions into an economic model:

Table 1: Simplifying Assumptions

Applying these assumptions, and signifying the real growth rate as , leads to the model shown in Equation

         

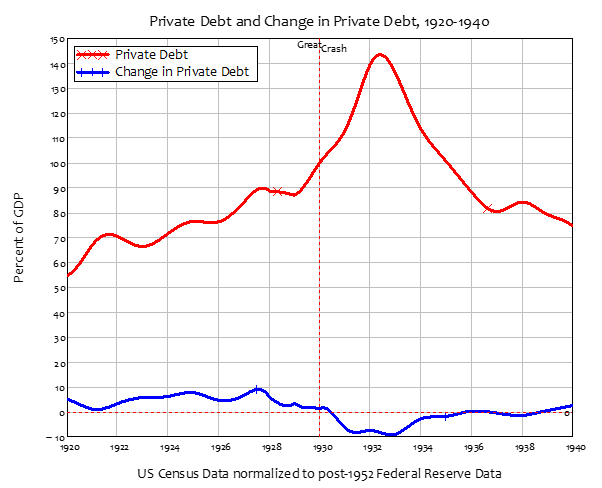
As shown in Appendix B, this inherently nonlinear model has two meaningful equilibria: one with a positive employment rate, positive wages share, and debt to GDP ratio, which Grasselli & Costa Lima dubbed the “good equilibrium”; another with zero employment, zero wages share, and an infinite debt to GDP ratio, which they dubbed the “bad equilibrium” (Grasselli and Costa Lima 2012).

The key parameter that determines the stability of these two equilibria is the slope of the investment function. With a low desire to invest ()—which, on the surface, would appear to imply a poorer level of economic performance—the “good equilibrium” is stable with equilibrium values of (see Figure 1), with the system converging over a large number of cycles.

Figure 1: Simulation with : convergence to the “good equilibrium”

However, with a high desire to invest ()—which, on the surface, would appear to imply a higher level of economic performance—the “good equilibrium” is unstable, with equilibrium values of (see Figure 2).

Figure 2: Simulation with : a “Great Moderation” followed by rising cycles and breakdown

The approach to, and then repulsion from, the good equilibrium follows what is known as the “intermittent route to chaos” (Pomeau and Manneville 1980), in which systemic turbulence appears to decline, only to subsequently rise once more. This reproduces several of the stylized facts of recent macroeconomic data:

• A rising level of private debt compared to GDP;
• An initial apparent decline in the volatility of employment, growth and wage demands—a “Great Moderation”—followed by increasing volatility and (ultimately) an economic collapse—a “Great Recession”; and
• Rising inequality, as the increased share going to bankers (in this three-class system) comes at the expense not of capitalists—who are the only ones borrowing in this simple model—but at the expense of the workers’ share of income.

A simple model derived directly from macroeconomic definitions thus reproduces the essence of Minsky’s FIH: the faster cyclical growth of debt relative to income over a series of credit-driven boom and bust cycles, leading to a period of increasing volatility and, in this model without bankruptcy or government, ultimate a terminal economic breakdown.

One essential aspect of this model is the proposition that the change in debt finances part of investment, and thus part of aggregate demand—loans are not “pure redistributions” (Bernanke 2000, p. 24) as portrayed in Neoclassical literature, but increases in bank assets which simultaneously create both money and additional aggregate demand and income. This can be proven using the key macroeconomic identity that expenditure is income.

The role of credit in aggregate demand and aggregate income

Central Banks have recently relieved Post Keynesian economists of the necessity of insisting that their “Endogenous Money” model of banking behaviour is structurally correct (Holmes 1969; Moore 1979; Moore 1988; Moore 1988; Dow 1997; Rochon 1999; Fullwiler 2013), while the Neoclassical models of “Loanable Funds” and the “Money Multiplier” are incorrect (McLeay, Radia et al. 2014; Deutsche Bundesbank 2017).

However, though the endogeneity of money is fully accepted in Post Keynesian and MMT circles, the macroeconomic significance of Endogenous Money is not. For instance, in a recent blog post, Wray argued that “in retrospect the endogenous money literature is trivial for several reasons”, with its implications largely being confined to how central banks set interest rates (Wray 2019). Similarly, in the debate in the Review of Keynesian Economics over an earlier, initially flawed, and more complicated expression of the arguments in this section (Fiebiger 2014; Keen 2014; Lavoie 2014; Palley 2014; Keen 2015), Fiebiger treated passages in which Minsky attempted to establish a role in aggregate demand for a change in the money supply (caused by a change in debt) as simply expressing a tautology:

Given the parameters specified, Minsky‘s (Minsky 1975, p. 133) deduction that ΔMt must be the source of growth allows Yt ex ante > Yt–1 ex post to be viewed as a tautology. (Fiebiger 2014, p. 295)

In the following tables (which I term “Moore Tables” in honour of Basil Moore), I use the key macroeconomic identity that expenditure is income to show that endogenous money is far from macroeconomically trivial, and that Minsky’s comments in (Minsky 1975, p. 133) and (Minsky 1982, pp. 3-6 in a section entitled “A sketch of a model”) were not tautological, but critical insights whose expression was hampered by the use of period analysis (Fontana 2003; Fontana 2004), as were Fiebiger’s attempts to interpret them. These tables show flows in continuous time, including credit, which I define as the time derivative of debt:

         

As in any differential equation, these flows are measured instantaneously, and dimensioned in the relevant time unit, which is dollars per year. I know that this is a foreign concept to a discipline accustomed to thinking in terms of periods, normally of a year: doesn’t one have to measure for a year to speak of, for example, credit per year? In fact, one does not. A monetary flow can be measured at an instant in time in terms of dollars per year, just as a car’s speedometer measures velocity at an instant in time in terms of kilometres per hour: since velocity is the time derivative of distance, if an instantaneous velocity of 100km/hr were maintained for an hour, then the vehicle would cover 100 kilometres in that hour. The same principle applies to the near instantaneous measurement of financial flows, even though they are the sum of a large number of discrete but asynchronous transactions sampled across a very small instant of time.

Each row in a Moore Table shows expenditure by one sector on the others in an economy. Expenditure is shown as a negative entry on the diagonal of the table, and a positive entry on the off-diagonal, with the two necessarily summing to zero on each row and the overall table. The negative sum of the diagonal of the table is aggregate demand , while the sum of the off-diagonal elements is aggregate income . The two are necessarily equal: expenditure is income.

Figure 3 shows a monetary economy in which neither lending nor borrowing can occur. The flows A to F represent the turnover of an existing and constant money stock, and in this sense are comparable to Friedman’s mythical “Optimum Quantity of Money” economy (Friedman 1969), though minus the helicopters dispensing money. The sum of these monetary flows can thus be substituted by the velocity of money V times the stock of money M, as in Equation .

Figure 3: Moore Table for a monetary economy with no lending

         

Figure 4 shows the mythical (McLeay, Radia et al. 2014) Neoclassical model of Loanable Funds, in which lending is between one non-bank agent and another. Lending is shown as a flow across the diagonal of the Moore Table. Without loss of generality, I show Sector 2 lending Credit dollars per year to Sector 1, which Sector 1 then spends buying the output of Sector 3; Sector 1 also has to pay Interest $/year to Sector 1, to service the outstanding stock of debt. The flow of lending affects the spending power of the lender as well as the borrower: the flow of Credit $/Year from Sector 2 to Sector 1 reduces the amount that Sector 2 can spend on Sector 3.

Figure 4: Moore Table for Loanable Funds

The sum of either the off-diagonal elements of Figure 4 (or the negative of the sum of the diagonal) confirms the belief of Neoclassical economists, that if banks were just intermediaries, then credit would be a pure redistribution, and it would play no role in aggregate demand and income. However, one interesting result is that (gross) interest payments are part of aggregate demand and aggregate income—see Equation .

         

Figure 5 shows the real-world situation that Credit money is created by bank lending. The Table is now expanded to show the Assets, Liabilities and Equity of the Banking Sector, and monetary flows now include the matching increase of Assets and Liabilities when a new loan (Credit, denominated in $/Year) is made, as well as transfers between Liabilities (predominantly deposit accounts), and also Bank Equity. The Credit money created by the loan is used by Sector 1 to buy goods from Sector 3, and Sector 1 is obliged to service the stock of outstanding loans by paying the flow of Interest $/Year to the Bank (which is recorded in its Equity account).

Figure 5: Moore Table for Endogenous Money (“Bank Originated Money and Debt”)

The crucial result here is that Credit is part of both aggregate demand and aggregate income, in the real world of Endogenous Money in which bank lending creates money:

         

This realisation strengthens the underlying Post Keynesian and MMT methodologies. Not only is “Endogenous Money/BOMD” a more realistic description of banking than “Loanable Funds”, it has an enormous impact on macroeconomics as well. Macroeconomic models that omit banks, debt, money—and therefore the role of credit in aggregate demand and income—omit the “causa causans that factor which is most prone to sudden and wide fluctuation” (Keynes 1936, p. 221), and are utterly misleading models of the macroeconomy. This judgment applies to the entire corpus of Neoclassical economics, bar the work of Michael Kumhof (Kumhof and Jakab 2015; Kumhof, Rancière et al. 2015).

Simulating Loanable Funds and BOMD

The macroeconomic significance of BOMD can be easily illustrated by converting a simple model of Loanable Funds in Minsky to a model of BOMD. The Loanable Funds model is fashioned on the model in (Eggertsson and Krugman 2012), where the consumer sector lends to the investment sector via a bank which operates as an intermediary, and which charges an introduction fee to the consumer sector. The model is completed by the employment of workers by both sectors, intermediate goods purchases by each sector from the other, and purchases of goods by workers and bankers.

The five accounts in the banking sector’s Godley Table are Reserves on its Assets side, three deposit accounts on its Liabilities—one each for the Consumer Sector , Investment Sector and workers —and the Bank’s Equity account . The transaction of lending, repayment, interest payments and the bank fee all operate through the Liability side of the Banking sector’s ledger: its Assets are unaffected (see Figure 6).

Figure 6: Banking sector view of Loanable Funds

Conversely, the financial operations all occur on the Asset side of the Consumer (lending) sector’s Godley Table (see Figure 7). Lending reduces the amount of money in the consumer sector’s deposit account, and increases the debt that the investment sector owes to it (see Figure 7).

Figure 7:Consumer (lender) sector view of Loanable Funds

For the borrower, the financial operations alter its Assets and its Liabilities equally. Credit increases its Asset the deposit account it has with the Banking Sector, and identically increases its liability of , its debt to the consumer sector (see Figure 8).

Figure 8: The Investment Sector’s (borrower’s) view of the economy

The core differential equations of this model, shown in Equation , can be derived directly by summing the columns of Figure 6 and Figure 7 (the flows that will be affected by the later conversion of this model to BOMD are highlighted in red):

         

All flows are defined in terms of first-order time lags related to the relevant account. In particular, lending by the consumer sector is shown as being based on the amount left in its bank account , while repayment by the Investment Sector is based upon the level of outstanding debt :

         

The parameters and are time constants, which can be varied during a simulation: reducing increases the speed of lending while reducing increases the speed of repayment. These are varied in the simulation shown in Figure 10. Substantial variations in the speed of lending and repayment dramatically alter the private debt to GDP ratio, but only transiently affect economic activity.

This simulation confirms the Neoclassical conditional logic that, if banks were mere intermediaries as Loanable Funds portrays them to be, then banks, debt and money could be ignored in macroeconomics. Large changes in credit have negligible impact upon GDP growth—and in fact credit and GDP growth move in opposite directions in this simulation, because the borrower has been given a lower overall propensity to spend than the lender, so that an increase in lending actually reduces GDP via a fall in the velocity of money (and vice-versa: see Figure 9).

Figure 9: Loanable Funds in Minsky. Credit has no significant impact on macroeconomics

This was done to illustrate Bernanke’s assertion that, when lending is simply a “pure redistribution” (Bernanke 2000, p. 24), any macroeconomic impact of lending depends on differences in the marginal spending propensities of the lender and borrower. With the macroeconomic impact of credit depending on idiosyncratic characteristics of the borrower and lender, there is no systemic benefit for including banks, debt, and arguably, money, in macroeconomic theory for a world in which Loanable Funds is true.

Figure 10: Varying lending & repayment rates in Loanable Funds; no significant macroeconomic effects

However, in the real world, banks originate money and debt, and the impact of banks, debt and money on macroeconomics is highly significant. This can be illustrated by making the technically minor but systemically huge changes needed to convert this model of Loanable Funds into Bank Originated Money and Debt (BOMD)—by shifting debt from being an asset of the Consumer Sector to an asset of the Banking Sector (and deleting the superfluous “Fee”, since the Banking Sector now gets its income from the flow of interest). Credit thus increases the Assets of the banking sector and its Liabilities (the sum in the Investment Sector’s account ) by precisely the same amount.

Figure 11: Banking sector view of BOMD

The financial equations of this system are shown in Equation . These are simpler than the equations for Loanable Funds: the mythical intermediation is deleted, the three financial operations are removed from the equation for , and the interest payment now goes to the Banking Sector’s Equity account

         

These structural changes are the only differences between the two models in this paper. Strictly speaking, the flow of new debt should have been redefined, but this was left as is, to illustrate that the change in the structure of lending alone is sufficient to drastically transform macroeconomics from a discipline in which banks, debt and money can be ignored, into one in which they are critical.

Figure 12: Bank Originated Money and Debt in Minsky. Credit plays a critical role in macroeconomics

These simple structural changes lead to credit having an enormous impact on the economy. Credit and GDP growth now move in the same direction, and GDP grows when credit is positive and falls when it is negative. In keeping with the logical analysis of the previous section, credit adds to aggregate demand and income when it is positive, and subtracts from it when it is negative.

Figure 13: Varying lending & repayment parameters in BOMD: significant macroeconomic effects

Accounting for the Great Moderation & the Great Recession

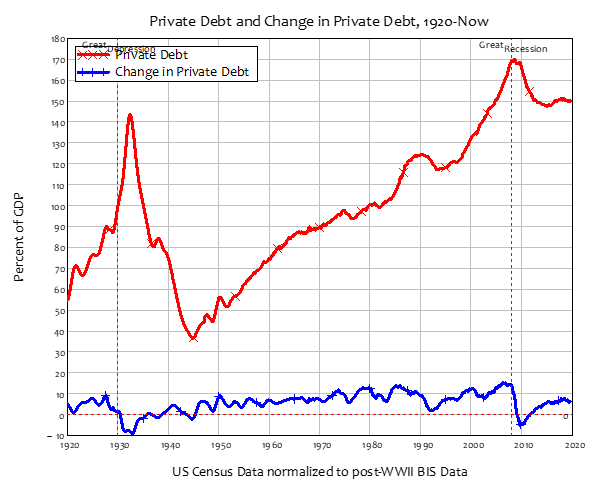
The models and logical analysis of the previous three sections provide a causal argument for a relationship between the levels of debt and credit and macroeconomics, and in particular, the experience of severe economic crises like the 2008 “Great Recession”. A rising level of debt relative to GDP, and a rising significance of credit relative to GDP, are Minskian warnings of a crisis, while the crisis is caused by a plunge in credit from strongly positive to strongly negative. The plunge in credit from a peak of 15% of GDP in late 2006 to a depth of -5% in late 2009 was the first experience of negative credit since the end of WWII, and this was the cause of the Great Recession.

Figure 14: The “Great Recession” was the first negative credit event in post-WWII economic history

The empirical relationship between credit and the level of unemployment rises as the level of private debt rises, and by the time of the recovery from the 1990s recession, it is overwhelming: in a ridiculously strong contrast to Bernanke’s Neoclassical a priori dismissal of Fisher’s Debt Deflation explanation for the Great Depression on the grounds that “Absent implausibly large differences in marginal spending propensities among the groups, it was suggested, pure redistributions should have no significant macroeconomic effects” (Bernanke 2000, p. 24), the correlation between credit and unemployment since 1990 is a staggering -0.85 (see Figure 15).

Figure 15: Credit and Unemployment. Correlation -0.53 since 1970, -0.85 since 1990

––p

The role of negative credit in the USA’s major economic crises

Since credit has no role in mainstream economic theory, the collection of data on private debt and credit has been sporadic, depending more on the initiative of statisticians than the expressed needs of economists for data. This situation has improved dramatically in recent years thanks to the work of the Bank of International Settlements (Borio 2012; Dembiermont, Drehmann et al. 2013), the Bank of England (Hills, Thomas et al. 2010) and various non-mainstream economists (Jorda, Schularick et al. 2011; Schularick and Taylor 2012; Vague 2019), but much remains to be done to provide the comprehensive time series data that the significance of debt and credit warrants.

However, some data can still be retrieved that helps make sense of past economic crises (Vague 2019). In particular, a long term debt series can be derived for the USA from three very different time series: the post-1952 Federal Reserve Flow of Funds data; Census data for debt between 1916 and 1970; and a series on loans by selected banks between 1834 and 1970 (Census 1949; Census 1975).

Figure 16: Debt to GDP data from the BIS & US Census

Fortunately, the data series overlap, and the trends in the data show that, though the definitions differed, the same fundamental processes were being tracked by these three data series. This allows a composite time series to be assembled by rescaling the two Census data series to match the current BIS/Federal Reserve data set. When credit data is derived from this composite series, two phenomena stand out: firstly, America’s greatest economic crises are caused by sustained periods of negative credit; and secondly, the post-WWII regime has only one negative credit event—the “Great Recession”—while the pre-WWI regime had frequent, though smaller, negative credit experiences (see Figure 17). The two greatest were the Great Depression, and the “Panic of 1837” (Roberts 2012).

While Great Depression and the Great Recession are etched into our collective memories, I was personally unaware of the “Panic of 1837” until this credit data alerted me to the scale of negative credit at that time. Though the recorded level of private debt was low compared to post-WWII levels, the rate of decline of debt—the scale of negative credit—was both enormous and sustained. Credit was negative between mid-1837 and 1844, and hit a maximum rate of decline of 9% of GDP. It is little wonder that the “Panic of 1837” was described as “an economic crisis so extreme as to erase all memories of previous financial disorders” (Roberts 2012, p. 24).

Figure 17: Composite time series for private debt and credit derived from the data in Figure 16

Nonlinearity and Realism

The model in Equation generates symmetric cycles—booms that are as big as busts, before a final collapse—simply because of the unrealistic assumption, made for reasons of analytic tractability, of linear behavioural relations (assumptions 7 & 8 in Table 1). Realistically, workers wage demands given the level of employment are nonlinear, as Phillips insisted (Phillips 1954; Phillips 1958), as are the investment reactions of capitalists to the rate of profit, as Minsky insisted with his perceptive concept of “euphoric expectations” (Minsky 1982, p. 140).

Keen’s 1995 Minsky model (Keen 1995) used the hyperbolic nonlinear function suggested by Blatt (Blatt 1983, p. 213) to avoid unrealistic outcomes, such as the employment rate exceeding 100% in a nonlinear Goodwin model (Goodwin 1967). A generalized exponential function can be used instead (see Equation ), which could allow unrealistic values. However, these are avoided by suitable choices of input variables (the employment to population ratio rather than the unemployment rate in the “Phillips Curve” function).

         

The parameters shown in Table 2 (stable wages at 60% employment, a slope of 2 for the wage change function at 60% employment, and a maximum wage decline of 4% per annum; investment 3% of GDP at 3% profit rate, investment function slope at 3% of 2, and a minimum gross investment level of zero) generate an asymmetric process in which the ultimate downturns are deeper than the booms. Nonlinear behavioural assumptions thus improve the realism of the model, but do not change its fundamental properties, which emanate from the inherent structural nonlinearity of the model itself.

Table 2: Nonlinear behavioural functions for wage change and investment

Extending the definitions to include inflation

A simple single-price-level nominal extension can be derived from definitions in the same fashion as the model in Equation , though it takes more assumptions to turn the definitional dynamic statements into a model. The definition of the employment rate is unchanged, while the definitions of the wages share of GDP and the debt to GDP ratio are both in monetary terms:

         

When differentiated with respect to time, this yields three definitionally true statements as before, but this time the rate of change of prices is a component of two of them:

• The employment rate will rise if real economic growth exceeds the sum of population growth and growth in labor productivity;
• The wages share of output will rise if money wage demands exceed the sum of inflation and growth in labor productivity; and
• The private debt to GDP ratio will rise if the rate of growth of private debt exceeds the sum of inflation plus the rate of economic growth.

In equations, these statements are:

         

where the subscript R signifies “real” as opposed to monetary.

Conclusion: the macroeconomic foundations of macroeconomics

Minsky’s Financial Instability Hypothesis is thus not merely a particular Post Keynesian model, but a foundational model of macroeconomics, in the same sense that Lorenz’s model of turbulence in fluid dynamics is a foundational model for meteorology (Lorenz 1963). Though Minsky did not do this himself, a model of his hypothesis can be derived directly from the impeccably sound macroeconomic foundations of incontestable macroeconomic definitions. It can be extended in the same manner, by adding definitions for government spending, asset price dynamics that differ from commodity price dynamics, multi-sectoral production, etc. The structure and history of an economy are the primary drivers of its behaviour, rather than the behaviour of individual agents in it. “Agents” are, as Marx famously remarked, constrained by history:

Men make their own history, but they do not make it as they please; they do not make it under self-selected circumstances, but under circumstances existing already, given and transmitted from the past. The tradition of all dead generations weighs like a nightmare on the brains of the living. (Marx 1852, Chapter 1)

System dynamics enables the modelling of the structure, the history, and the dynamics of the economy. Minsky’s genius was that he perceived, without this technology, the essential elements of all three that make capitalism prone to crises. Minsky and system dynamics therefore provide the foundations for a paradigmatic challenge to Neoclassical economics, whose development has been driven by the obsession with finding sound microfoundations for macroeconomics, all the while ignoring results that showed this was impossible (Gorman 1953; Anderson 1972; Sonnenschein 1972; Sonnenschein 1973). Macrofoundations, far-from-equilibrium complex systems dynamics, and monetary analysis—the polar opposites of the Neoclassical obsessions with microfoundations, equilibrium and barter—are the proper bases for economic theory.

Postscript: Minsky the Software

All the models in this paper have been built in Minsky, which is an Open Source system dynamics program with the unique feature enabling financial flows to be modelled easily—and their structure modified easily—using interlocking double-entry bookkeeping tables called “Godley Tables” (in honour of Wynne Godley). Minsky can be downloaded from SourceForge, or its Patreon page. The developers would appreciate it if specialists on Minsky the economist—and Post Keynesian economists in general—would download Minsky the software, and help to extend it further by providing user feedback.

Appendix

1. Continuous versus discrete time
   

A referee suggested that discrete-time difference equations were more appropriate “for problems which are specified in terms of accounting relationships (which are discrete)”, and that continuous-time differential equations “gives rise to nonobvious relationships in the structure of delays. What kind of profit does finance investment? Obviously past profit; but the specification in continuous-time does not allow to make it evident.”

While each individual financial transaction is discrete, each is also asynchronous with other financial transactions. In a “top down” model, aggregate asynchronous phenomena are more realistically modelled using continuous time than discrete time: this is why aggregate population growth models use continuous time, even though each birth is a discrete event.

The time delays in discrete time economic models are also normally arbitrary. They are almost always in terms of years, which is reasonable for investment, but not for consumption, where the scale should be in terms of weeks or months rather than years. To do discrete-time modelling properly, consumption in period t should be modelled as depending on income in period t-2 (say), where the time period is measured in weeks, while investment in period t should be modelled as depending on the change in income between period t-26 and t-52 (say).

But firstly, no-one does this, because it is simply too complicated: in practice, lags of one year are commonplace in macroeconomic discrete time models. Secondly, if this were done, and empirical work later found that investment in period t actually depended on the change income between period t-40 and t-86 (say), then entire structure of the model would need to be re-written. This is not necessary for a continuous time model, where the equivalent function to a time delay is a time lag. The dependence of, for example, investment today on profits in the past, could be shown using a linear first order time lag: a new variable is defined (say, ) which is shown as converging to the actual variable with a time lag of , where the value of is measured in years:

         

The scalar can be altered in a continuous time model without having to alter the structure to the model itself.

Time lags were not used in the model derived from macroeconomic definitions, because the objective was to produce the simplest possible model working from those definitions, and because time lags introduce dynamics of their own, independent of the structural points made by that model. However, time lags were integral to the models of Loanable Funds and Bank Originated Money and Debt (BOMD), in which they linked the outstanding stocks to the flows. The full equation for the rate of change of private debt in the BOMD model is:

         

Here is the length of time that new lending would take to double D if it occurred at a linear rate, while tells how long repayment would take to reduce D to zero if it occurred at a linear rate. For more on discrete vs continuous time modelling, and time lags in economic modelling, see (Andresen 2018).

1. Stability analysis of basic Minsky model
   

The basic Minsky model is:

         

The following shorthand expressions are used in this model with linear behavioural functions:

         

Spelling out these shorthand expressions yields the fully specified model, which makes it easier to identify the nonlinear feedbacks in this model. Instances where the system states interact nonlinearly with each other are highlighted in red: there are two dampening nonlinear feedbacks in the equation for , one amplifying feedback for , and two amplifying feedbacks for (including one term in ).

         

The “good” equilibrium of this model is more easily derived by solving for the zeros of these equations via the substitution that (with ):

         

This equilibrium is in terms of the profit share, employment rate and debt ratio: the wages share is a derivative of these, since . This residual role for the wages-share of output manifests itself in the model dynamics as well: before the crisis, the wages share falls as the debt level rises, while the profit share fluctuates around its equilibrium. This confirms Marx’s intuition in Capital I that wages are a dependent variable in capitalism: “To put it mathematically: the rate of accumulation is the independent, not the dependent, variable; the rate of wages, the dependent, not the independent, variable” (Marx 1867, Chapter 25, Section 1).

The stability of the system about its equilibria are given by its Jacobian, which, given the system’s 3 dimensions and 10 parameters, is very complicated. Making the substitutions that , it is

         

 

Substituting numerical values for all but the key parameter yields the characteristic polynomial of the Jacobian in terms of :

         

This has one real eigenvalue which is always negative, and two complex eigenvalues which have zero or negative real parts for values of , and positive real parts for : see Figure 18. The system thus bifurcates at this point, changing from one where the “good equilibrium” is stable and a cyclical attractor, to one where it is unstable and a cyclical repeller: the system converges towards it under the influence of the negative real eigenvalue until, in proximity to this equilibrium, the real parts of the complex eigenvalues repel the system, which then explosively converges to the “bad equilibrium”.

Figure 18: Eigenvalues for π_S=6 & 6.1, as calculated symbolically in Mathcad

1. Loanable Funds & BOMD
   

The key differential equations for the models of Loanable Funds and BOMD as shown in Equations and respectively. The definitions they share are shown in Equation :

         

1. Distinguishing Debt from Credit
   

Kalecki once famously remarked that economics was “the science of confusing stocks with flows” (Robinson 1982, p. 295). That is apparent in the confusion caused by the use of the word “Credit” to describe both the level of debt (in $) and its rate of change (in $/year). An outstanding example of this is the paper “The Economic Crisis from a Neoclassical Perspective” (Ohanian 2010), by the prominent “New Classical” economist Lee Ohanian, in which he rules out the “financial explanation” of the 2008 crisis on the basis of the following empirical argument:

The financial explanation also argues that the 2007-2009 recession became much worse because of a significant contraction of intermediation services. But some measures of intermediation have not declined substantially. Figure 4, which is updated from Chari, Christiano, and Kehoe (Chari, Christiano et al. 2008), shows that bank credit relative to nominal GDP rose at the end of 2008 to an all-time high. And while this declined by the first quarter of 2010, bank credit was still at a higher level at this point than any time before 2008… These data suggest that aggregate quantities of intermediation volumes have not declined markedly. (Ohanian 2010, p. 59)

Ohanian’s Figure 4 is reproduced below. It is obvious from the scale that the data he used recorded the stock of outstanding debt, rather than the flow of new debt: if new debt had indeed been between 1.2 and 2 times GDP every year since 1978, then private debt would have been many hundreds to thousands of times GDP by 2010. He—and Chari, Christiano, and Kehoe before him (Chari, Christiano et al. 2008; Troshkin 2008)—interpreted that stock as a flow, in part because the word “credit” was used to describe it—and also of course because this error suits the non-monetary analysis of Neoclassical economics. On the basis of this obvious error, Ohanian (and Chari, Christiano, and Kehoe before him) reject the argument that the financial crisis of 2008 was in fact a financial crisis.

To avoid this stock-flow confusion, I use the word “Debt” to describe the level of debt, dimensioned in currency units, and “Credit” to describe the flow of new debt, dimensioned in currency units per year. I recommend this practice to other Post Keynesians.

References

Anderson, P. W. (1972). “More Is Different.” Science
177(4047): 393-396.

Andresen, T. (2018). On the Dynamics of Money Circulation, Creation and Debt – a Control Systems Approach. Engineering Cybernetics, Norwegian University of Science and Technology.

Baran, P. A. (1968). Monopoly capital an essay on the American economic and social order / Paul A. Baran and Paul M. Sweezy. New York, New York : Monthly Review Press.

Bernanke, B. S. (2000). Essays on the Great Depression. Princeton, Princeton University Press.

Blanchard, O. (2018). “On the future of macroeconomic models.” Oxford Review of Economic Policy
34(1-2): 43-54.

Blatt, J. M. (1983). Dynamic economic systems: a post-Keynesian approach. Armonk, N.Y, M.E. Sharpe.

Borio, C. (2012) “The financial cycle and macroeconomics: What have we learnt?” BIS Working Papers.

Census, B. o. (1949). Historical Statistics of the United States 1789-1945. B. o. t. Census. Washington, United States Government.

Census, B. o. (1975). Historical Statistics of the United States Colonial Times to 1970. B. o. t. Census. Washington, United States Government.

Chari, V., L. Christiano, et al. (2008). “Facts and myths about the financial crisis of 2008.” IDEAS Working Paper Series from RePEc.

Charles, S. (2005). “A Note on Some Minskyan Models of Financial Instability.” Studi Economici
60(86): 43-51.

Charles, S. (2008). “Teaching Minsky’s Financial Instability Hypothesis: A Manageable Suggestion.” Journal of Post Keynesian Economics
31(1): 125-138.

Cruz, M. (2005). “A Three-Regime Business Cycle Model for an Emerging Economy.” Applied Economics Letters
12(7): 399-402.

Dembiermont, C., M. Drehmann, et al. (2013). “How much does the private sector really borrow? A new database for total credit to the private nonfinancial sector.” BIS Quarterly Review(March): 65-81.

Deutsche Bundesbank (2017). “The role of banks, non- banks and the central bank in the money creation process.” Deutsche Bundesbank Monthly Report: 13-33.

Dow, S. C. (1997). Endogenous Money. A “second edition” of The general theory. G. C. Harcourt and P. A. Riach. London, Routledge. 2: 61-78.

Eggertsson, G. B. and P. Krugman (2012). “Debt, Deleveraging, and the Liquidity Trap: A Fisher-Minsky-Koo approach.” Quarterly Journal of Economics
127: 1469–1513.

Fazzari, S., P. Ferri, et al. (2008). “Cash Flow, Investment, and Keynes-Minsky Cycles.” Journal of Economic Behavior and Organization
65(3-4): 555-572.

Fiebiger, B. (2014). “Bank credit, financial intermediation and the distribution of national income all matter to macroeconomics.” Review of Keynesian Economics
2(3): 292-311.

Fontana, G. (2003). “Post Keynesian Approaches to Endogenous Money: a time framework explanation.” Review of Political Economy
15(3).

Fontana, G. (2004). “Hicks on monetary theory and history: money as endogenous money.” Cambridge Journal of Economics
28: 73-88.

Friedman, M. (1969). The Optimum Quantity of Money. The Optimum Quantity of Money and Other Essays. Chicago, MacMillan: 1-50.

Fullwiler, S. T. (2013). “An endogenous money perspective on the post-crisis monetary policy debate.” Review of Keynesian Economics
1(2): 171–194.

Gatti, D. D., D. Delli Gatti, et al. (1994). Financial Institutions, Economic Policy, and the Dynamic Behavior of the Economy. Levy Economics Institute of Bard College Working Papers. Annandale-on-Hudson, NY, Levy Economics Institute.

Goodwin, R. M. (1967). A growth cycle. Socialism, Capitalism and Economic Growth. C. H. Feinstein. Cambridge, Cambridge University Press: 54-58.

Gorman, W. M. (1953). “Community Preference Fields.” Econometrica
21(1): 63-80.

Grasselli, M. and B. Costa Lima (2012). “An analysis of the Keen model for credit expansion, asset price bubbles and financial fragility.” Mathematics and Financial Economics
6: 191-210.

Hicks, J. (1981). “IS-LM: An Explanation.” Journal of Post Keynesian Economics
3(2): 139-154.

Hicks, J. R. (1937). “Mr. Keynes and the “Classics”; A Suggested Interpretation.” Econometrica
5(2): 147-159.

Hills, S., R. Thomas, et al. (2010). “The UK recession in context — what do three centuries of data tell us?” Bank of England Quarterly Bulletin
2010 Q4: 277-291.

Holmes, A. R. (1969). Operational Constraints on the Stabilization of Money Supply Growth. Controlling Monetary Aggregates. F. E. Morris. Nantucket Island, The Federal Reserve Bank of Boston: 65-77.

Jarsulic, M. (1989). “Endogenous credit and endogenous business cycles.” Journal of Post Keynesian Economics
12: 35-48.

Jorda, O., M. Schularick, et al. (2011). “Financial Crises, Credit Booms, and External Imbalances: 140 Years of Lessons.” IMF Economic Review
59(2): 340-378.

Jorgenson, D. W. (1960). “A Dual Stability Theorem.” Econometrica
28(4): 892-899.

Jorgenson, D. W. (1961). “Stability of a Dynamic Input-Output System.” The Review of Economic Studies
28(2): 105-116.

Jorgenson, D. W. (1963). “Stability of a Dynamic Input-Output System: A Reply.” The Review of Economic Studies
30(2): 148-149.

Keen, S. (1995). “Finance and Economic Breakdown: Modeling Minsky’s ‘Financial Instability Hypothesis.’.” Journal of Post Keynesian Economics
17(4): 607-635.

Keen, S. (2014). “Endogenous money and effective demand.” Review of Keynesian Economics
2(3): 271–291.

Keen, S. (2015). “The Macroeconomics of Endogenous Money: Response to Fiebiger, Palley & Lavoie.” Review of Keynesian Economics
3(2): 602 – 611.

Keynes, J. M. (1936). The general theory of employment, interest and money. London, Macmillan.

Kumhof, M. and Z. Jakab (2015). Banks are not intermediaries of loanable funds — and why this matters. Working Paper. London, Bank of England.

Kumhof, M., R. Rancière, et al. (2015). “Inequality, Leverage, and Crises.” The American Economic Review
105(3): 1217-1245.

Lavoie, M. (2014). “A comment on ‘Endogenous money and effective demand’: a revolution or a step backwards?” Review of Keynesian Economics
2(3): 321 – 332.

Lorenz, E. N. (1963). “Deterministic Nonperiodic Flow.” Journal of the Atmospheric Sciences
20(2): 130-141.

Lucas, R. E., Jr. (2004). “Keynote Address to the 2003 HOPE Conference: My Keynesian Education.” History of Political Economy
36: 12-24.

Marx, K. (1852). The Eighteenth Brumaire of Louis Bonaparte. Moscow, Progress Publishers.

Marx, K. (1867). Capital. Moscow, Progress Press.

Marx, K. (1894). Capital Volume III, International Publishers.

McLeay, M., A. Radia, et al. (2014). “Money creation in the modern economy.” Bank of England Quarterly Bulletin
2014 Q1: 14-27.

McManus, M. (1963). “Notes on Jorgenson’s Model.” The Review of Economic Studies
30(2): 141-147.

Minsky, H. P. (1957). “Monetary Systems and Accelerator Models.” The American Economic Review
47(6): 860-883.

Minsky, H. P. (1975). John Maynard Keynes. New York, Columbia University Press.

Minsky, H. P. (1982). Can “it” happen again? : essays on instability and finance. Armonk, N.Y., M.E. Sharpe.

Moore, B. J. (1979). “The Endogenous Money Stock.” Journal of Post Keynesian Economics
2(1): 49-70.

Moore, B. J. (1988). “The Endogenous Money Supply.” Journal of Post Keynesian Economics
10(3): 372-385.

Moore, B. J. (1988). Horizontalists and Verticalists: The Macroeconomics of Credit Money. Cambridge, Cambridge University Press.

Ohanian, L. E. (2010). “The Economic Crisis from a Neoclassical Perspective.” Journal of Economic Perspectives
24(4): 45-66.

Palley, T. (2014). “Aggregate demand, endogenous money, and debt: a Keynesian critique of Keen and an alternative theoretical framework.” Review of Keynesian Economics
2(3): 312–320.

Phillips, A. W. (1954). “Stabilisation Policy in a Closed Economy.” The Economic Journal
64(254): 290-323.

Phillips, A. W. (1958). “The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom, 1861-1957.” Economica
25(100): 283-299.

Piketty, T. (2014). Capital in the Twenty-First Century. Harvard, Harvard College.

Pomeau, Y. and P. Manneville (1980). “Intermittent transition to turbulence in dissipative dynamical systems.” Communications in Mathematical Physics
74: 189-197.

Roberts, A. (2012). America’s first Great Depression: economic crisis and political disorder after the Panic of 1837. Ithaca, Cornell University Press.

Robinson, J. (1982). “Shedding darkness.” Cambridge Journal of Economics
6(3): 295-296.

Rochon, L.-P. (1999). “The Creation and Circulation of Endogenous Money: A Circuit Dynamique Approach.” Journal of Economic Issues
33(1): 1-21.

Rosser, J. B. (1999). Chaos Theory. Encyclopedia of Political Economy. P. A. O’Hara. London, Routledge. 2: 81-83.

Santos, C. H. D. and A. C. Macedo e Silva (2009). ‘Revisiting (and Connecting) Marglin-Bhaduri and Minsky–An SFC Look at Financialization and Profit-led Growth’, Levy Economics Institute, The, Economics Working Paper Archive.

Schularick, M. and A. M. Taylor (2012). “Credit Booms Gone Bust: Monetary Policy, Leverage Cycles, and Financial Crises, 1870-2008.” American Economic Review
102(2): 1029-1061.

Schumpeter, J. A. (1954). History of economic analysis / Joseph A. Schumpeter / edited from manuscript by Elizabeth Boody Schumpeter. London, London : Allen & Unwin.

Sonnenschein, H. (1972). “Market Excess Demand Functions.” Econometrica
40(3): 549-563.

Sonnenschein, H. (1973). “Do Walras’ Identity and Continuity Characterize the Class of Community Excess Demand Functions?” Journal of Economic Theory
6(4): 345-354.

Taylor, L. and S. A. O’Connell (1985). “A Minsky Crisis.” Quarterly Journal of Economics
100(5): 871-885.

Troshkin, M. (2008). “Facts and myths about the financial crisis of 2008 (Technical notes).” IDEAS Working Paper Series from RePEc.

Tymoigne, E. (2006). ‘The Minskyan System, Part III: System Dynamics Modeling of a Stock Flow-Consistent Minskyan Model’, Levy Economics Institute, The, Economics Working Paper Archive.

Vague, R. (2019). A Brief History of Doom: Two Hundred Years of Financial Crises. Philadelphia, University of Pennsylvania Press.

Wray, L. R. (2019). “Response to Doug Henwood’s Trolling in Jacobin.” New Economic Perspectives
http://neweconomicperspectives.org/2019/02/response-to-doug-henwoods-trolling-in-jacobin.html.

 

 

I had a very nice chat with the Canadian blogger Steve Saretsky about my economic analysis, largely as applied to Canada. Click on the link above to see it; I’ve copied it here in case Patreon stuffs up as it did on my “Eve of Destruction” post.

I shared my screen a few times to show data relevant to Canada. One of the obvious questions was “how did Canada manage to avoid a crisis in 2008 while its southern neighbour had such a big one?”. The answer was “because you kept your private debt bubble going while the USA’s ended”. Here are the charts that I put together to support that case. I’ve also attached the data to this post.

Friends, Romans, countrymen, lend me your ears;
I come to bury Caesar, not to praise him.
The evil that men do lives after them;
The good is oft interred with their bones;
So let it be with Caesar. (Marc Antony’s funeral oration in Shakespeare’s Julius Caesar, Act III, Scene II)

Introduction

As aficionados of Shakespeare know, Marc Antony’s speech was ironic: his aim really was to praise Caesar. My intention, however, really is burial: the multiplier-accelerator model of business cycles really does need to be buried, as an “evil that men do” which should not have lived on even during the lives of the Caesars of economics who gave birth to it—specifically, Alvin Hansen, Paul Samuelson (Samuelson 1939; Samuelson 1939) and John Hicks (Hicks 1949; Hicks 1950). We should instead resurrect in its place the “Growth Cycle” model of one of the neglected greats of economics, Richard M. Goodwin (Goodwin 1966; Goodwin 1967). Difference equation methods, which are integral to the multiplier-accelerator model and which still dominate economic modelling, should also give way to differential equations and system dynamics. In making this argument, I showcase Goodwin’s model and extensions of it in the Open Source system dynamics program Minsky.

Zombienomics: the undead Multiplier-Accelerator model should die

The Australian economist John Quiggin coined the term Zombie Economics to characterize ideas that should have died out in economics, but nonetheless persist (Quiggin 2010). Most of Quiggin’s nominations of Zombie economic ideas were the application of faulty economic theories (such as the “Efficient Markets Hypothesis”) to economic policy (such as the deregulation of finance markets). The multiplier-accelerator model has not led to specific policies. However, it has helped to mislead economists about the manner in which economic dynamics should be practised, and in so doing it has possibly caused as much harm as any specific misguided economic policy.

The continuing citations of the source articles by Samuelson (Samuelson 1939; Samuelson 1939)—64 citations for “Synthesis” and 356 for “Interactions”, according to the Web of Science database, with the latter paper clearly undergoing a unfortunate revival in popularity since the start of the millennium—are proof that the Multiplier-Accelerator model still walks amongst us is (see Figure 1).

Figure 1: Citations over time of “Interactions between the multiplier analysis and the principle of acceleration”

Equally significant is the model’s presence as Chapter 11 in Quantitative Economics with Python (Sargent and Stachurski 2020), an Open Source online textbook co-authored by the “Nobel” Prize-winning economist , Thomas Sargent. The multiplier-accelerator model does not play a significant role in modern economics in general, or DSGE modelling in particular, but it is indicative of the poor attention to realism, and obsession with faux and dated analytic techniques, that Paul Romer (another recipient of what I prefer to call the “Faubel Prize in Economics”) (Mirowski 2020) rightly savages in his brilliant but unfortunately unpublished monograph “The Trouble with Macroeconomics” (Romer 2016).

Much of the equilibrium-fixated methodology and pedagogy that our book hopes to replace with system dynamics methods and training originate in the teaching materials written and seminars run by Sargent and his followers. As well as being dominated by equilibrium methods, the fundamental mathematical techniques in both Quantitative Economics with Python and its “advanced” companion Advanced Quantitative Economics with Python (Sargent and Stachurski 2020) are restricted to difference equations, rather than differential equations. In fact, differential equations are not mentioned at all in the “Advanced” text, and are noted just once, in passing, in Quantitative Economics with Python, when complex numbers are discussed. The mention is in relation to the use of complex numbers in determining the properties of the multiplier-accelerator model:

“Useful and interesting in its own right, these concepts reap substantial rewards when studying dynamics generated by linear difference equations or linear differential equations. For example, these tools are keys to understanding outcomes attained by Paul Samuelson (1939) [93] in his classic paper on interactions between the investment accelerator and the Keynesian consumption function, our topic in the lecture Samuelson Multiplier Accelerator.” (Sargent and Stachurski 2020, p. 47).

Samuelson’s paper was indeed a classic: a classic mistake, which should finally be laid to rest. Sargent and Stachurski set out the model’s derivation as follows:

“The model combines the consumption function

         

with the investment accelerator

         

and the national income identity

         

• The parameter 𝑎
is peoples’ marginal propensity to consume out of income…

• The parameter > 0 is the investment accelerator coefficient…

Equations (1), (2), and (3) imply the following second-order linear difference equation for national income:

         ”

(Sargent and Stachurski 2020, p. 189)

To analyze the model, they set 𝐺𝑡 and 𝛾 to zero, and apply the method of characteristic equations, which converts the difference equation:

         

into the quadratic:

         

The roots of this quadratic are:

         

These roots generate several different classes of behaviour—damped oscillations, explosive growth, explosive oscillations, explosive growth—depending on the magnitudes of its parameters. But these are meaningless characteristics of a meaningless model, as can easily be shown using a more sophisticated mathematical technique, of converting a high order scalar difference equation to a system of first order vector difference equations.

In general, to convert an n^th order difference equation to a set of first order equations, you define a vector whose components are:

         

The model can now be restated using a matrix of coefficients:

         

The advantage of this technique over the characteristic equation approach is that it imposes a check on the validity of a model, before a characteristic equation is derived: for a model to be valid, the determinant of , where I is the identity matrix, must be zero. If it is not, then the model’s equilibrium is zero. If we consider an equilibrium vector , then it must be true that:

         

If then cannot be inverted, and can have non-trivial values. If then can be inverted, and the only solution is “the trivial solution”, and therefore there is something wrong with the model: it is asking a question whose only general answer is “zero”.

The matrix form of the multiplier-accelerator model is shown in Equation :

         

This fails the non-trivial solution test:

         

Therefore, there must be something wrong with derivation of the multiplier-accelerator model itself.

There are in fact at least two things wrong, the most serious of which is the mis-specification of actual investment in Equation . The national income identity describes the sum of actual consumption and actual investment (and actual government spending , the last of which is omitted in the analysis). Actual investment is defined as the change in the capital stock, and in a discrete-time model investment in time is added to capital stock at time to create the capital stock for period +1:

         

If we want to relate this to the term in Equation , which fundamentally defines desired investment rather than actual investment, then we need to relate the capital stock to output . The simplest way to do this is to presume a linear capital to output ratio , so that:

         

To instead use Equation as the expression for investment in year t, as is done in the “multiplier-accelerator model”, the following equation must hold:

         

The only way this can be guaranteed to hold for any non-zero values of , are that ; the only way to guarantee that it holds for non-zero values (when in general ) are that . This is the primary reason why this model only has the trivial solution: it is asking the question “under what conditions can actual investment be guaranteed to equal desired investment, when both are different linear functions of change in output between different years?”. The answer is “when output is zero, and therefore when investment never occurs”. Clearly, this is not the basis on which to erect a model of cycles!

The other problem with the “model” is its treatment of time, which is an unavoidable consequence of the discrete-time formulation of the model. The definition of Consumption in Equation , relates it to the last time period’s income . This would be valid if the time period was of the order of a week to a month: it is reasonable to assume that aggregate consumption is a function of the previous week to month’s income, given that the vast majority of consumers are wage-earners living from paycheck to paycheck. But with a time-dimension measured in weeks or months, the relation for investment makes no sense: investment has a time horizon of years, not months—let alone weeks. Since investment is the driving factor in this “model”, its time dimension must dominate, in which case it makes no sense to relate consumption to last year’s income: it should be treated as related to this year’s income instead:

         

If we combine this reasonable postulate for consumption in a discrete-time model with the definition of actual investment in Equation via the truncated national income identity (ignoring for simplicity), we get

         

This is a first-order growth relationship, not a model of cycles.

If economics even remotely resembled a science, it would consign the multiplier-accelerator model to its rubbish heap. Since it is not, I have zero faith that this “model” will be abandoned: economists will continue teaching it, regardless of the fact that it has rotten foundations. True progress in dynamics will only come from those outside the mainstream paradigm, and in disciplines like system dynamics. In the remainder of this chapter I want to alert genuine practitioners of dynamics to the existence of a model that has impeccable foundations, which can be used as the basis for well-grounded structural models of capitalism, but which—predictably—has been ignored by mainstream economists. This is Richard Goodwin’s “Growth cycle” model (Goodwin 1967). Unlike the “multiplier-accelerator model”, this model is mathematically valid (the proof is left as an exercise for the reader!), and as such it can be used as the foundation for more realistic models.

Goodwin’s Growth Cycle model and the Keen-Minsky extension

In contrast to the prominence and fawning treatment given to Samuelson’s model, Goodwin’s model was published only in a single-page precis to a supplementary (conference proceedings) volume of the leading mainstream journal Econometrica (Goodwin 1966), as a brief chapter in an edited book (Goodwin 1967), and as a chapter in a book of Goodwin’s collected essays (Goodwin 1982). The Web of Science database records zero citations of this paper in any form. This is of course wrong—I have personally cited it in numerous times, as has Grasselli (Grasselli and Costa Lima 2012; Grasselli and Maheshwari 2017) and several other authors (Landesmann, Goodwin et al. 1994; Harvie, Kelmanson et al. 2007; Flaschel 2015; Giraud and Grasselli 2019)—but it indicates the risible lack of attention paid to this model compared to Samuelson’s.

Goodwin developed his model as a way of expressing Marx’s unexpected cyclical model of growth in Capital I, Chapter 25:

Or, on the other hand, accumulation slackens in consequence of the rise in the price of labour, because the stimulus of gain is blunted. The rate of accumulation lessens; but with its lessening, the primary cause of that lessening vanishes, i.e., the disproportion between capital and exploitable labour power. The mechanism of the process of capitalist production removes the very obstacles that it temporarily creates. The price of labour falls again to a level corresponding with the needs of the self-expansion of capital, whether the level be below, the same as, or above the one which was normal before the rise of wages took place. (Marx 1867, p. 437)

While its origins in Marx may put some readers off, far from being based on any necessarily “Marxist” vision of capitalism, and in contrast to the logically false “multiplier-accelerator model”, Goodwin’s growth cycle can be derived from the impeccable foundations of uncontestably true macroeconomic definitions. We start from the definitions of the employment rate , which is the ratio of the number of people with a job to the total population ; and the wages share of GDP , which is the total wage bill divided by GDP :

         

Simple calculus turns these static definitions into dynamic statements that are also true by definition: “the employment ratio will rise if employment grows faster than population”; and “the wages share of GDP will grow if wages grow faster than GDP”. Using for , these statements are:

         

These dynamic definitions can be turned into a model via one more definition, and a set of genuinely simplifying assumptions. We define the ratio of output to labour ; we assume a constant capital to output ratio ; we assume all profits are invested, so that gross investment equals profits (this simplifying assumption is relaxed in the subsequent model); depreciation occurs at a constant rate ; a uniform real wage applies; there is a linear relationship between the employment rate and the rate of change of real wages; and both the output to labour ratio and population grow at the exogenously given rates and respectively. We also define the profit share of output and the gross investment to output ratio :

         

These assumptions let us expand out the rates of change expressions for and (the rate of change of is by assumption):

         

Feeding these into Equation gives us the basic Goodwin model:

         

This model generates both growth and cycles, as the title of Goodwin’s paper states. Figure 2 illustrates the basic dynamics of this model in the Open Source system dynamics program Minsky (which can be downloaded from https://sourceforge.net/projects/minsky/).

Figure 2: The basic Goodwin model in Minsky

This is using a system dynamics program to express a set of differential equations. Precisely the same dynamics can be shown by using Minsky in the traditional causal diagram approach of system dynamics:

InvestmentàRate of change of CapitalàOutputàEmploymentàRate of change of the wageàWagesàProfitàInvestment

In this method, the employment rate and wages share of GDP become calculated variables, while the capital stock , wage rate , output to labor ratio and population are defined by integral blocks—see Figure 3.

Figure 3: Goodwin’s growth cycle model as a flowchart

I used Goodwin’s model as the foundation for my model of Minsky’s Financial Instability Hypothesis (Keen 1995), taking my lead from Blatt’s observation that Goodwin’s model was remarkably successful “Considering the extreme crudity of some of the assumptions underlying this model”, and that its main weakness of “an equilibrium which is not unstable (it is neutral) … can be remedied [by the] introduction of a financial sector, including money and credit as well as some index of business confidence” (Blatt 1983, p. 210).

Minsky thought of the economy in historical rather than merely logical time, with history determining current expectations, and with feedbacks from current conditions changing both the economy and expectations over a cycle:

The natural starting place for analyzing the relation between debt and income is to take an economy with a cyclical past that is now doing well. The inherited debt reflects the history of the economy, which includes a period in the not too distant past in which the economy did not do well. Acceptable liability structures are based upon some margin of safety so that expected cash flows, even in periods when the economy is not doing well, will cover contractual debt payments. As the period over which the economy does well lengthens, two things become evident in board rooms. Existing debts are easily validated and units that were heavily in debt prospered; it paid to lever… (Minsky 1977, p. 10)

A period of tranquil growth thus leads to rising expectations, and a tendency to increase leverage. As Minsky put it in his most famous sentence:

Stability ‒ or tranquility ‒ in a world with a cyclical past and capitalist financial institutions is destabilizing. (Minsky 1977, p. 10).

Minsky’s basic vision was clearly tailor-made for dynamic modelling, but he failed to do this himself, primarily because he chose a poor foundation for it—specifically, Samuelson’s multiplier-accelerator model! (Minsky 1957). I used the far better foundation of Goodwin’s model, and extended it to consider financial dynamics by:

• Redefining profit to be net of interest payments as well as of wages; and
• Introducing a nonlinear investment function based on the rate of profit.

As with Goodwin, a Minsky model can be derived directly from macroeconomic definitions, once it is accepted that banks create money when they create loans (McLeay, Radia et al. 2014), and that that newly created money adds to aggregate demand and income (Keen 2015). We then add the definition of to our fundamental macroeconomic identities, where D is the level of private debt.

The simplest assumption for the causal process behind change in debt is that new debt is used to finance investment in excess of profits—something which has been empirically confirmed by, of all people, Eugene Fama (Fama and French 1999), one of the main promulgators of the Efficient Markets Hypothesis (Fama 1970; Fama and French 2004). Profits are now net of interest payments on debt as well as of wages, while investment is a linear function of the rate of profit:

         

As with the wages share and the employment rate, the definition of the debt ratio is easily turned into a dynamic statement that “the debt ratio will rise if debt grows faster than GDP”:

         

We already have from Equation , so only needs to be derived:

         

Substituting this into Equation yields:

         

This gives us a 3-dimensional model:

         

 

As Li and Yorke proved almost half a century ago, “Period Three Implies Chaos” (Li and Yorke 1975), and that is what this model manifests. There are two meaningful equilibria, a “good equilibrium” with a positive employment rate, wages share of GDP, and a finite debt to GDP ratio, and a “bad equilibrium” (Grasselli and Costa Lima 2012, p. 208) with a zero rate of employment and wages share of GDP and an infinite debt ratio, The former equilibrium is stable for low values of the slope of the investment function, with one negative and two complex eigenvalues with zero real part. However, as the slope of the investment function steepens, the two complex eigenvalues develop a positive real part, and “good equilibrium” becomes unstable—but remains an attractor for the early part of the model’s trajectory. The model then demonstrates the chaotic behavior first observed in fluid dynamics and described as the “intermittent route to chaos” by Pomeau and Manneville (Pomeau and Manneville 1980): cycles diminish for a while, only to rise later on—see Figure 4.

Figure 4: The basic Minsky cycle, modelled in Minsky

When I first developed this model (in August of 1992), I saw its characteristic of diminishing and then rising cycles as its most striking feature. This was not a prediction of Minsky’s verbal model: though he expected a set of cycles before an ultimate one that would lead to a debt-deflationary crisis like the Great Depression—in the absence of “big government” (Minsky 1982, p. xxix)— he made no claim that the cycles themselves would get smaller before the crisis. Nor was it a feature of the economic data at that time. This coincidence inspired what I thought at the time was the rhetorical flourish with which that paper concluded:

From the perspective of economic theory and policy, this vision of a capitalist economy with finance requires us to go beyond that habit of mind that Keynes described so well, the excessive reliance on the (stable) recent past as a guide to the future. The chaotic dynamics explored in this paper should warn us against accepting a period of relative tranquility in a capitalist economy as anything other than a lull before the storm. (Keen 1995, p. 634)

Then reality imitated the model: there was indeed a period of diminishing cycles in the employment rate, growth rate and inflation rate, which Neoclassical economists dubbed “The Great Moderation”, and for which they took the credit (Stock and Watson 2002; Bernanke 2004; Srinivasan 2008). Then there was a crisis, which Neoclassical economists dubbed “The Great Recession”, and which they blamed on exogenous shocks (Ireland 2011).

In contrast, rather that requiring two independent explanations for real world phenomena, this simple model captures the essential features of recent economic data—including the rise in the private debt ratio, and the fall in workers’ share of GDP (see Figure 5)—in one inherently nonlinear system.

Figure 5: Reality imitates the Keen-Minsky model

This extremely simple and well-grounded model clearly provides a better foundation for dynamics than the equilibrium-fixated, difference equation models that dominate Neoclassical macroeconomics today. That will not stop Neoclassicals persisting with DSGE modelling, but the unreasonable effectiveness of these simple models should encourage critics and student rebels to ignore the intellectual backwater of Neoclassical economics, and to develop well-grounded system dynamics models of capitalism instead.

Modelling Money, and the Coronavirus, in Minsky

Though Minsky has some obvious advantages over existing system dynamics programs—the mathematics-oriented GUI, using variables names as well as wires to build equations, the unique capacity to format text using L^AT_EX, overloading of mathematical operators to reduce clutter, the embedding of plots in the design canvas, plots that update dynamically where parameters can be varied during a simulation, etc.—its main is its capacity to model financial dynamics using interlocking double-entry bookkeeping tables called Godley Tables. These take statements of flows between financial accounts and generate systems of differential equations that are guaranteed to be correct. It is also much easier to edit financial flows using a Godley Table than it is to edit them when they are defined using the standard system dynamics flowchart interface.

For example, Figure 6 shows the financial flows in a simple model of the reality that bank loans create deposits—the opposite of the textbook story in which banks are passive “intermediators” who lend out deposits (McLeay, Radia et al. 2014). The table simply records flows between one bank account and another, with Minsky checking that “Assets minus Liabilities minus Equity equals Zero” (the final column in the table).

Figure 6: Godley Table for a simple model of the macroeconomics of Bank Originated Money and Debt (McLeay, Radia et al. 2014)

Neither differential equations nor the customary stock and flow blocks of standard system dynamics programs appear in a Godley Table, but in the background, Minsky turns these flow entries into ODEs of the financial system that are guaranteed to be consistent. Each equation below is the sum of the relevant column in the Godley Table above:

         

The model is completed by defining the individual flow components using flowchart operators. Figure 7 shows a simulation run of this “Bank Originated Money and Debt” model in which flows are related to the levels of accounts via the engineering concept of time constants. The rates of lending and repayment are varied during the simulation by altering the value of the time constants for lending and repayment, using sliders that are intrinsic to every parameter in Minsky.

Figure 7: A simulation run of the Bank Originated Money and Debt model

In addition to being an excellent foundation for monetary stock-flow consistent models (Lavoie and Godley 2001; Lavoie 2014), Godley Tables can be used whenever a model has the requirement that the entities being modelled cannot be in two states at one time, so that flows between system states are exclusive: a flow must go from one state to another. In the context of the current Coronavirus crisis, they can be repurposed to model a pandemic, since the “Susceptible, Exposed, Infected, Recovered, Dead” or SIERD epidemiological models also have that requirement.

The basic SIR model of susceptibility, infection and recovery (Kermack, McKendrick et al. 1927 [1997]) can be seen as an extension of the predator-prey model, in which the consequence of predation is not death but infection. In the basic predator-prey model, an assumed exponential growth of the prey population x at a rate is reduced by a constant times , the prey population, so that . Interaction between the predator and prey is thus shown as a multiplicative relationship.

In modelling a pandemic, the population N is normally treated as a constant, since it changes far less rapidly than the epidemic spreads. The rate of change of the fraction of the population that is infected depends on the interactions of those infected I with those susceptible S, which in turn depends on the frequency of both groups in the overall population, and , and the transmissibility of the disease, which is modelled by the parameter :

         

Since population is treated as constant, this reduces to:

         

Since the increase in those infected is equal to the fall in those who are susceptible, the rate of growth of those infected is the negative of the rate of decline of those susceptible, minus the recovery rate R, which is modelled as a parameter times the number infected:

         

Figure 8 shows this model implemented in Minsky, using time constants rather than parameters. The Godley Table’s tabular format makes it easy to see the interrelations between the Susceptible, Infected and Recovered compartments. Flowchart tools are only needed to define the flows themselves (and future versions will allow these to be defined off the canvas, using standard L^AT_EX equation notation).

Figure 8: Simple SIR model of a pandemic

The Godley Table interface also makes it very easy to extend this model to a more realistic situation in which there is a more complicated transmission chain—see Figure 9. Other comparmentalizations—such as dividing the susceptible population into the general public and medical staff, including quarantined versus non-quarantined, hospitalized versus non-hospitalized, etc.—are equally straightforward to add and define.

Figure 9: SEIRD model developed by editing Godley Table of SIR model

A 3^rd order revision of the multiplier-accelerator model

I hesitate to write this section, because I wish to bury, not merely the invalid multiplier-accelerator model itself, but also the practice of using difference equations to model the economy, when continuous time system dynamics methods are so much more suitable (Keen 2006). However, it would be intellectually dishonest not to note that the multiplier-accelerator model can be saved to some degree by doing what Hansen, Samuelson and Hicks did not do: by paying proper attention to the causal process between their hypothetical equation for desired investment, and actual investment, capital stock, and output.

In this model, I use Samuelson’s (Samuelson 1939) function for desired investment, which he modelled as a lagged response to changes in consumption in the previous two years:

         

Here c is the desired “incremental capital to output ratio” (ICOR) (Walters 1966) and s the savings rate. I then assume that these investment plans are carried out, so that this becomes the change in capital in year , which is added to the existing stock in year to yield the capital stock in year .

         

Using the accelerator relation between capital and output, his results in a third order difference equation for Y:

         

Though I do not wish to encourage the further development of this model, it certainly has many interesting characteristics when compared to Samuelson’s invalid 2^nd order model. Firstly, it is a meaningful model: the determinant of minus the first-order vector form of this equation is zero, as is required. Secondly, its characteristic equation is

         

This is easily factored into three components which are also easily interpreted: the first means that any sustained level of output is an equilibrium; the second root determines the growth rate, and the third creates cycles which remain smaller than and proportional to the growth rate.

Thirdly, in a very non-Neoclassical (and pro-Keynesian!) result, an increase in the savings rate causes a fall in the rate of economic growth. Also, for sustained growth to occur, c—which determines desired investment—must substantially exceed the actual ICOR. With a lower level for c or a slightly higher value for s, a non-equilibrium set of initial conditions leads to a convergence to a new, higher equilibrium level. See Figure 10 for a comparison of two simulations with slightly different savings ratios.

Figure 10: Cyclical growth in the 3rd order Multiplier-Accelerator Model, with a higher savings rate meaning lower growth

 

Conclusion

I fervently hope that dynamics has a better future in economics than it has had a past. But the odds are not good. We should be under no illusion that the methodology we champion will be resisted by Neoclassical economists, who have, over time, and largely unconsciously, turned equilibrium from the unfortunate compromise in methodology that Jevons, Marshall and even Walras knew it to be, into a religion about the tendencies of actual capitalism.

Almost fifty years ago, the authors of the Limits to Growth (Meadows, Randers et al. 1972) naively expected that the system dynamics methodology that Forrester had developed (Forrester 1968; Forrester 1971) and that they had applied would be welcomed by economists, as a way of escaping from the dead-end of having to pretend that equilibrium applied in order to model dynamic processes. They were unprepared for the ferocity of the attack on their methodology by Neoclassical economists, and most prominently by William Nordhaus (Nordhaus 1973; Forrester, Gilbert et al. 1974; Nordhaus, Stavins et al. 1992).

Since then, economics has, if anything, gone backwards. As the 2018 recipient of “The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel” Paul Romer observed, in his working paper “The Trouble With Macroeconomics”, mainstream macroeconomic modelling is so divorced from reality today that it deserves to be called not merely “post-modern” but “post-real”:

Lee Smolin begins The Trouble with Physics (Smolin 2007) by noting that his career spanned the only quarter-century in the history of physics when the field made no progress on its core problems. The trouble with macroeconomics is worse. I have observed more than three decades of intellectual regress…

Macroeconomists got comfortable with the idea that fluctuations in macroeconomic aggregates are caused by imaginary shocks, instead of actions that people take, after Kydland and Prescott (1982) launched the real business cycle (RBC) model…

In response to the observation that the shocks are imaginary, a standard defense invokes Milton Friedman’s methodological assertion from unnamed authority that “the more significant the theory, the more unrealistic the assumptions (p.14).” More recently, “all models are false” seems to have become the universal hand-wave for dismissing any fact that does not conform to the model that is the current favorite. The noncommittal relationship with the truth revealed by these methodological evasions … goes so far beyond post-modern irony that it deserves its own label. I suggest “post-real.” (Romer 2016).

Critical perspectives like Romer’s from within the mainstream might give us hope, but the belief that he criticizes—that the economy can and indeed should be described as an equilibrium system occasionally disturbed by exogenous shocks—is still the majority belief within the mainstream. An example of the ferocity with which this belief is held is V.V. Chari’s defence of DSGE (“Dynamic Stochastic General Equilibrium”) models before the US Congress in 2010, after their abject failure to anticipate the “Great Recession” of 2008:

All the interesting policy questions involve understanding how people make decisions over time and how they handle uncertainty. All must deal with the effects on the whole economy. So, any interesting model must be a dynamic stochastic general equilibrium model. From this perspective, there is no other game in town… A useful aphorism in macroeconomics is: “If you have an interesting and coherent story to tell, you can tell it in a DSGE model. If you cannot, your story is incoherent.” (Chari 2010, p. 2)

From the perspective of a genuine mathematician, this is nonsense: the addiction to equilibrium modelling is the main weakness of economics, not its strength. The brilliant applied mathematician John Blatt put it this way in 1983:

In defense of this concentration on equilibrium and the neglect of true dynamics, there are two arguments:

1. Statics or (what comes to much the same thing) balanced proportional growth is much easier to handle theoretically than true dynamic phenomena. A good understanding of statics is a necessary prerequisite for the study of dynamics. We must learn to walk before we can attempt to run.

2. In any case, while no economic system is ever in strict equilibrium, the deviations from such a state are small and can be treated as comparatively minor perturbations. The equilibrium state is, so to speak, the reference state about which everything turns and toward which the system gravitates. Market prices fluctuate up and down, but there exist “natural prices” about which this fluctuation occurs, and these natural prices can be determined directly, by ignoring the fluctuations altogether and working as if strict equilibrium obtained throughout.

Such arguments did carry a great deal of conviction two hundred years ago, when the basic ideas of the science of economics were being formulated for the first time. However, it is impossible to ignore the passage of two hundred years. A baby is expected to first crawl, then walk, before running. But what if a grown-up man is still crawling? At present, the state of our dynamic economics is more akin to a crawl than to a walk, to say nothing of a run. Indeed, some may think that capitalism as a social system may disappear before its dynamics are understood by economists. (Blatt 1983, pp. 4-5. Emphasis added)

When I first read this passage, I regarded it as an excellent piece of hyperbole. Now, almost 40 years later, as capitalism itself is in intensive care thanks to Covid-19, and with signs of climate change abounding in phenomena like the unprecedented wildfires in Australia in 2019-20 (Dowdy, Ye et al. 2019), it is beginning to feel amazingly prescient. This makes the task of establishing genuinely dynamic, non-equilibrium methods in economics even more pressing, despite the near-religious defence of equilibrium modelling by mainstream economists themselves.

References

Bernanke, B. S. (2004). The Great Moderation: Remarks by Governor Ben S. Bernanke At the meetings of the Eastern Economic Association, Washington, DC February 20, 2004. Eastern Economic Association. Washington, DC, Federal Reserve Board.

Blatt, J. M. (1983). Dynamic economic systems: a post-Keynesian approach. Armonk, N.Y, M.E. Sharpe.

Chari, V. V. (2010). Building a science of economics for the real world. Subcommittee on investigations and oversight , Committee on science and technology. U. Congress. Washington, U.S. Government printing office.

Dowdy, A. J., H. Ye, et al. (2019). “Future changes in extreme weather and pyroconvection risk factors for Australian wildfires.” Scientific Reports
9(1).

Fama, E. F. (1970). “Efficient Capital Markets: A Review of Theory and Empirical Work.” The Journal of Finance
25(2): 383-417.

Fama, E. F. and K. R. French (1999). “The Corporate Cost of Capital and the Return on Corporate Investment.” Journal of Finance
54(6): 1939-1967.

Fama, E. F. and K. R. French (2004). “The Capital Asset Pricing Model: Theory and Evidence.” The Journal of Economic Perspectives
18(3): 25-46.

Flaschel, P. (2015). “Goodwin’s MKS system: a baseline macro model.” Cambridge Journal Of Economics
39(6): 1591-1605.

Forrester, J. W. (1968). “Industrial Dynamics-After the First Decade.” Management Science
14(7): 398-415.

Forrester, J. W. (1971). World Dynamics. Cambridge, MA, Wright-Allen Press.

Forrester, J. W., W. L. Gilbert, et al. (1974). “The Debate on “World Dynamics”: A Response to Nordhaus.” Policy Sciences
5(2): 169-190.

Giraud, G. and M. Grasselli (2019). “Household debt: The missing link between inequality and secular stagnation.” Journal of Economic Behavior & Organization.

Goodwin, R. M. (1966). “Cycles and Growth: A growth cycle.” Econometrica
34(5 Supplement): 46.

Goodwin, R. M. (1967). A growth cycle. Socialism, Capitalism and Economic Growth. C. H. Feinstein. Cambridge, Cambridge University Press: 54-58.

Goodwin, R. M. (1982). Essays in economic dynamics by R. M. Goodwin. London, London : Macmillan.

Grasselli, M. and B. Costa Lima (2012). “An analysis of the Keen model for credit expansion, asset price bubbles and financial fragility.” Mathematics and Financial Economics
6: 191-210.

Grasselli, M. R. and A. Maheshwari (2017). “A comment on ‘Testing Goodwin: growth cycles in ten OECD countries’.” Cambridge Journal of Economics
41(6): 1761-1766.

Harvie, D., M. A. Kelmanson, et al. (2007). “A Dynamical Model of Business-Cycle Asymmetries: Extending Goodwin.” Economic Issues
12(1): 53-92.

Hicks, J. R. (1949). “Mr. Harrod’s Dynamic Theory.” Economica
16(62): 106-121.

Hicks, J. R. (1950). A Contribution to the Theory of the Trade Cycle. Oxford, Clarendon.

Ireland, P. N. (2011). “A New Keynesian Perspective on the Great Recession.” Journal of Money, Credit, and Banking
43(1): 31-54.

Keen, S. (1995). “Finance and Economic Breakdown: Modeling Minsky’s ‘Financial Instability Hypothesis.’.” Journal of Post Keynesian Economics
17(4): 607-635.

Keen, S. (2006). The Need and Some Methods for Dynamic Modelling in Post Keynesian Economics. Complexity, Endogenous Money and Macroeconomic Theory: Essays in Honour of Basil J. Moore. M. Setterfield. Edward Elgar, Cheltenham: 36-59.

Keen, S. (2015). “The Macroeconomics of Endogenous Money: Response to Fiebiger, Palley & Lavoie.” Review of Keynesian Economics
3(2): 602 – 611.

Kermack, W. O., A. G. McKendrick, et al. (1927 [1997]). “A contribution to the mathematical theory of epidemics.” Proceedings of the Royal Society of London A
115: 700–721.

Landesmann, M., R. Goodwin, et al. (1994). Productivity Growth, Structural Change and Macroeconomic Stability. Economic growth and the structure of long-term development: Proceedings of the IEA conference held in Varenna, Italy. New York, St. Martin’s Press: 205-240.

Lavoie, M. (2014). SFC modeling isn’t always easy! UMKC Conference on the Stock Flow Consistent Approach. UMKC, UMKC.

Lavoie, M. and W. Godley (2001). “Kaleckian Models of Growth in a Coherent Stock-Flow Monetary Framework: A Kaldorian View.” Journal of Post Keynesian Economics
24(2): 277-311.

Li, T.-Y. and J. A. Yorke (1975). “Period Three Implies Chaos.” The American Mathematical Monthly
82(10): 985-992.

Lucas Jr, R. E. and T. J. Sargent (1978). After Keynesian Macroeconomics. After The Phillips Curve: Persistence of High Inflation and High Unemployment. F. E. Morris. Boston, Federal Reserve Bank of Boston.

Marx, K. (1867). Capital. Moscow, Progress Press.

McLeay, M., A. Radia, et al. (2014). “Money creation in the modern economy.” Bank of England Quarterly Bulletin
2014 Q1: 14-27.

Meadows, D. H., J. Randers, et al. (1972). The limits to growth. New York, Signet.

Minsky, H. P. (1957). “Monetary Systems and Accelerator Models.” The American Economic Review
47(6): 860-883.

Minsky, H. P. (1977). “The Financial Instability Hypothesis: An Interpretation of Keynes and an Alternative to ‘Standard’ Theory.” Nebraska Journal of Economics and Business
16(1): 5-16.

Minsky, H. P. (1982). Can “it” happen again? : essays on instability and finance. Armonk, N.Y., M.E. Sharpe.

Mirowski, P. (2020). The Neoliberal Ersatz Nobel Prize. Nine Lives of Neoliberalism. D. Plehwe, Q. Slobodian and P. Mirowski. London, Verso: 219-254.

Nordhaus, W. D. (1973). “World Dynamics: Measurement Without Data.” The Economic Journal
83(332): 1156-1183.

Nordhaus, W. D., R. N. Stavins, et al. (1992). “Lethal Model 2: The Limits to Growth Revisited.” Brookings Papers on Economic Activity
1992(2): 1-59.

Pomeau, Y. and P. Manneville (1980). “Intermittent transition to turbulence in dissipative dynamical systems.” Communications in Mathematical Physics
74: 189-197.

Prescott, E. C. (1999). “Some Observations on the Great Depression.” Federal Reserve Bank of Minneapolis Quarterly Review
23(1): 25-31.

Quiggin, J. (2010). Zombie economics : how dead ideas still walk among us / John Quiggin. Oxford, Princeton University Press.

Romer, P. (2016). “The Trouble with Macroeconomics.” https://paulromer.net/trouble-with-macroeconomics-update/WP-Trouble.pdf.

Samuelson, P. A. (1939). “Interactions between the multiplier analysis and the principle of acceleration.” Review of Economic and Statistics
20: 75-78.

Samuelson, P. A. (1939). “A Synthesis of the Principle of Acceleration and the Multiplier.” Journal of Political Economy
47(6): 786-797.

Sargent, T. J. and J. Stachurski (2020). Advanced Quantitative Economics with Python.

Sargent, T. J. and J. Stachurski (2020). Quantitative Economics with Python.

Sargent, T. J. and N. Wallace (1976). “Rational Expectations and the Theory of Economic Policy.” Journal of Monetary Economics
2(2): 169-183.

Srinivasan, N. (2008). “From the Great Inflation to the Great Moderation: A Literature Survey.” Journal of Quantitative Economics, New Series
6(1-2): 40-56.

Stock, J. H. and M. W. Watson (2002). Has the business cycle changed and why? NBER Working Papers, National Bureau of Economic Research.

Walters, A. A. (1966). “Incremental Capital-Output Ratios.” The Economic Journal
76(304): 818-822.

 

 

I am writing a chapter on for a book on economic dynamics right now, and as I was doing so, I cited John Blatt‘s Dynamic Economic Systems, and lamented the fact that this brilliant book was out of print. But you never know, so I decided to check.

I was delighted to find that this is no longer a fact. On July 29, 2019, Dynamic Economic Systems: A Post Keynesian Approach was republished in Kindle format by Routledge (its Taylor and Francis division): here’s the link to it on their website: https://www.taylorfrancis.com/books/e/9781315496290.

I was a bit dubious when I first saw the link, because the abstract of the book—both on Amazon, and on Taylor & Francis’s website—was “The future of the Common Law judicial system in Hong Kong depends on the perceptions of it by Hong Kong’s Chinese population, judicial developments prior to July 1, 1997, when Hong Kong passes from British to Chinese control, and the Basic Law. These critical issues are addressed in this book.”. Really. But Blatt’s book is SO good that I thought I’d risk wasting the £24.66 and becoming more informed than I needed to be on Hong Kong.

Fortunately, there it was in all its glory, and brilliantly typeset—far better than the scanned version I’ve been relying upon for many years.

I urge my Patrons to buy a copy: I knew a lot of the history of economic thought and the mathematical methods that Blatt covers before I read this book, but Blatt taught me many things I didn’t know, and he gave me insights that I probably would never have acquired on my own. In particular, I had read Goodwin’s “A growth cycle” paper {Goodwin, 1967 #279} before reading Blatt, but really couldn’t make head nor tail of it: Goodwin was not a good writer. Fortunately, Blatt’s explanation of it was so clear, and so encouraging, that I used Goodwin’s model as the basis of my model of Minsky’s Financial Instability Hypothesis {Keen, 1995 #3316}. That model has been the basis of everything I’ve done in economics since. I wouldn’t have managed it without Blatt.

The book is superbly written, and Blatt handles the problem of communicating mathematics to economists—who know far less mathematics than they think they do—very well. Even if you can’t cope with the mathematics, it provides the best overview of the history of economic thought and the development (and retardation!) of economics that I have ever read. I aspire to writing as good a book as this when I finally pen my “magnum opus”.

I quote the first part of the book’s introduction below, to give you a feeling for its content, and Blatt’s extraordinarily clear writing style. Before it, I’ll provide one of my favorite anecdotes, in which Blatt stars: I wasn’t there to witness this event unfortunately, but I heard about it from many colleagues when I was studying both economics and mathematics while working at the University of New South Wales in the late 1980s and early 1990s. The antagonist in this story, Murray Kemp, was also a colleague then, and I have to emphasise, Murray was—and is—a thorough gentleman, and someone I was very glad to call a friend when I was there (he also beat me at tennis every time we played, so he was a top class sporting companion too). Murray suffers in the anecdote, and I can think of many other people whom I’d rather had been on the sharp end of Blatt’s famously sharp tongue than the very decent Murray. But the story is too good not to share, in this context.

Murray Kemp and John Blatt were both Professors at the University of New South Wales, Murray of Economics and John of Mathematics. Murray had been nominated for the “Nobel Prize in Economics” for his work on international trade theory, while Blatt had been nominated for the Nobel Prize in Physics. Neither got the award, but because of this coincidence, Murray regarded John as his one true peer at UNSW, and invited John to attend a seminar of his at the Department of Economics.

After Murray finished delivering his paper, he asked John what he thought of it. Blatt replied, in his heavily Austrian-accented English:
    “Zat is ze greatest load of rubbish that I have sat through in my professional career. If this is advanced economics, then there is something seriously wrong with the state of economics, and I intend finding out what it is.”

Some years later, this brilliant book was born. Buy a copy: you won’t regret it.

Introduction A. Purpose and limitations

The bicentenary of The Wealth of Nations has passed, and so has the centenary of the neoclassical revolution in economics. Yet the present state of dynamic economic theory leaves very much to be desired and appears to show little sign of significant improvement in the near future.

From the time of Adam Smith, economic theory has developed in terms of an almost universal concentration of thought and effort on the study of equilibrium states. These may be either states of static equilibrium, or states of proportional and balanced growth. Truly dynamic phenomena, of which the most striking example is the trade cycle, have been pushed to the sidelines of research.

In defense of this concentration on equilibrium and the neglect of true dynamics, there are two arguments:

1. Statics or (what comes to much the same thing) balanced proportional growth is much easier to handle theoretically than true dynamic phenomena. A good understanding of statics is a necessary prerequisite for the study of dynamics. We must learn to walk before we can attempt to run.

2. In any case, while no economic system is ever in strict equilibrium, the deviations from such a state are small and can be treated as comparatively minor perturbations. The equilibrium state is, so to speak, the reference state about which everything turns and toward which the system gravitates. Market prices fluctuate up and down, but there exist “natural prices” about which this fluctuation occurs, and these natural prices can be determined directly, by ignoring the fluctuations altogether and working as if strict equilibrium obtained throughout.

Such arguments did carry a great deal of conviction two hundred years ago, when the basic ideas of the science of economics were being formulated for the first time.

However, it is impossible to ignore the passage of two hundred years. A baby is expected to first crawl, then walk, before running. But what if a grown-up man is still crawling? At present, the state of our dynamic economics is more akin to a crawl than to a walk, to say nothing of a run. Indeed, some may think that capitalism as a social system may disappear before its dynamics are understood by economists.

It is possible, of course, that this deplorable lack of progress is due entirely to the technical difficulty of investigating dynamic systems and that economists, by following up the present lines of research, will eventually, in the long long long run, develop a useful dynamic theory of their subject.

However, another possibility must not be ignored. It is by no means true that all dynamic behavior can be understood best, or even understood at all, by starting from a study of the system in its equilibrium state. Consider the waves and tides of the sea. The equilibrium state is a tideless, waveless, perfectly flat ocean surface. This is no help at all in studying waves and tides. We lose the essence of the phenomenon we are trying to study when we concentrate on the equilibrium state. Exactly the same is true of meteorology, the study of the weather. Everything that matters and is of interest to us happens because the system is not in equilibrium.

In the first example, the equilibrium state is at least stable, in the sense that the system tends to approach equilibrium in the absence of disturbances. But there is no such stability in meteorology. The input of energy from the sun, the rotation of the earth, and various other effects keep the system from getting at all close to equilibrium. Nor, for that matter, would we wish it to approach equilibrium. The true equilibrium state, in the absence of heat input from the sun, is at a temperature where all life comes to a stop! The heat input from the sun is the basic power source for winds, clouds, etc., for everything that makes our weather. The heat input is very steady, but the resulting weather is not steady at all. None of this can be understood by concentrating on a study of equilibrium.

There exist known systems, therefore, in which the important and interesting features of the system are “essentially dynamic,” in the sense that they are not just small perturbations around some equilibrium state, perturbations which can be understood by starting from a study of the equilibrium state and tacking on the dynamics as an afterthought.

If it should be true that a competitive market system is of that kind, then the lack of progress in dynamic economics is no longer surprising. No progress can then be made by continuing along the road that economists have been following for two hundred years. The study of economic equilibrium is then little more than a waste of time and effort.

This is the basic contention of Dynamic Economic Systems. Its main purpose is to present arguments for this contention and to start developing the tools which are needed to make progress in understanding truly dynamic economic systems.

A subsidiary purpose, related to the main one but not identical with it, is to present a critical survey of the more important existing dynamic economic theories-in particular, the theories of balanced proportional growth and the theories of the trade cycle. This survey serves three purposes:

1. It is useful in its own right, as a summary of present views, and it can be used as such by students of economics.

2. It establishes contact between the new approach and the literature.

3. It is necessary to clear the path to further advance, which is currently blocked by beliefs which are very commonly held, but which are not in accordance with the facts.

The third point needs some elaboration. The main enemy of scientific progress is not the things we do not know. Rather, it is the things which we think we know well, but which are actually not so! Progress can be retarded by a lack of facts. But when it comes to bringing progress to an absolute halt, there is nothing as effective as incorrect ideas and misleading concepts. “Everyone knows” that economic models must be stable about equilibrium, or else one gets nonsense. 1 So, models with unstable equilibria are never investigated! Yet, in this as in so much else, what “everyone knows” happens to be simply wrong. Such incorrect ideas must be overturned to clear the path to real progress in dynamic economics.

This is a book on basic economic theory, addressed to students of economics. It is not a book on “mathematical economics,” and even less so a book on mathematical methods in economics. On the contrary, the mathematical level of this book has been kept deliberately to an irreducible, and extremely low, minimum. Chapters are literary, with mathematical appendices. The level of mathematics in the literary sections is the amount of elementary algebra reached rather early in high school; solving two linear equations in two unknowns is the most difficult mathematical operation used. In the mathematical appendices, the level is second year mathematics in universities; the meaning of a matrix, of eigenvalues, and of a matrix inverse are the main requirements. Whenever more advanced mathematics is required-and this is very rarely indeed-the relevant theorems are stated without proof, but with references to suitable textbooks. This very sparing use of mathematics should enable all economics students, and many laymen, to read and understand this book fully. Those who cannot follow the mathematical appendices must take the mathematics for granted, but if they are prepared to do that, they will lose nothing of the main message.

This does not mean that mathematics is unimportant or of little help, when used properly. This unfortunately all too common belief is incorrect. To make real progress in dynamic economics, researchers must know rather more, and somewhat different, mathematics from what is commonly taught to students of economics. But while mathematics is highly desirable, probably essential, to making further progress, the progress that has already been made can be phrased in terms understandable to people without mathematical background. This reliance on nonmathematical diction has not been easy for someone to whom mathematics is not some arcane foreign language, but rather his normal mode of thinking; only time can tell to what extent the effort has been successful.

Another limitation of this work is the restriction to classically competitive conditions in most cases. There is no discussion of monopoly, oligopoly, restrictions on entry, or related matters which are stressed, quite rightly, in the so-called post-Keynesian literature. This omission is not to be interpreted as disagreement with, or lack of sympathy for, the contentions of that school. Rather, the post-Keynesians have been entirely too kind and indulgent toward the neoclassical doctrine. The assumption of equilibrium has indeed been attacked (Robinson 1974, for example), but only in rather general terms. The more prominent part of the postKeynesian critique has been that conventional economic theory bases itself on assumptions (e.g., perfect competition, perfect market clearing, certainty of the future) which are invalid in our time, though some of them (not perfect certainty of the future!) may have been appropriate a century ago. We agree with this criticism, but that is not the point we wish to make in this book.

Rather, even under its own assumptions, conventional theory is incorrect. A competitive economic system with market clearing and certainty of the future does not behave in the way that theory claims it should behave. It is not true that, under these assumptions, the equilibrium state is stable and a natural center of attraction to which the system tends to return of its own accord. Obviously, in any such discussion, questions of oligopoly, imperfect market clearing, etc. are irrelevant. It is for that reason, and only for that reason, that such matters are ignored here.

In this view, the rise of oligopoly toward the end of the nineteenth century was not just an accident or an aberration of the system. Rather, it was a natural and necessary development, to be expected on basic economic grounds. John D. Rockefeller concealed his views on competition and paid lip service to prevailing ideas when it suited him. But he was a genius, who understood the system very well indeed and proved his understanding through phenomenal practical success. Alfred Marshall’s Principles of Economics was written and refined at the same time that Rockefeller established the Standard Oil trust and piloted it to an absolute dominance of the oil industry. There can be little doubt who had the better understanding of the true dynamics of the system.

It follows that the theory of this book should not be applied directly to conditions of monopoly or oligopoly, which are so prevalent in the twentieth century. However, the theory is directly relevant to something equally prevalent, namely the creation of economic myths and fairy tales, to the effect that all our present-day ills, such as unemployment and inflation, are due primarily to the mistaken intervention by the state in the working of what would otherwise be a perfect, self-adjusting system of competitive capitalism. This system was in power in the nineteenth century. It is wellknown that it failed to ensure either common equity (read Charles Dickens on the conditions under which little children were worked to death!) or economic stability: There were “panics” every ten years or so. The theory of this book shows that the failure of stability was not an accident, but rather was, and is, an inherent and inescapable feature of a freely competitive system with perfect market clearing. The usual equilibrium analysis assumes stability from the start, whereas actually the equilibrium is highly unstable in the long run. The economic myths pushed by so many interested parties are not only in contradiction to known history, but also to sound theory.

 

Blatt, John M.. Dynamic Economic Systems (pp. 4-8). Taylor and Francis. Kindle Edition.

I’m in a discussion on the New Zealand economy and the Coronavirus former Reserve Bank economist Michael Reddell this morning (Sunday) at 8.42AM on RNZ’s Sunday Morning show. I made a few observations about debt and the coronavirus. These charts are to help those who listen to the program follow my arguments.

The conventional model of infections is known as SEIR for “Susceptible/Exposed/Infected/Recovered”. This paper is one of many to produce such a model, with the relatively novel feature that it includes “resusceptibility”: the possibility that people who have been infected and have recovered might lose immunity and get it again.

Figure 1: The paper

In equations, it is as follows (in a simplified form omitting births and ordinary deaths, which is a reasonable simplifying assumption, given how quickly Covid-19 spreads):

Figure 2: The ordinary differential equations of the core model

Bryan Wisk, who is the founder of Asymmetric Return Capital, a long-time friend, and one of my patrons, volunteered to have this model developed by his staff in Minsky, and asked for some quick guidance on how to do so: hence this video. In it, I start to develop this model but don’t finish it—I’ll leave that for Bryan’s staff.

The paper itself has a “dashboard” of the model, but to run it, you need a copy of the commercial program in which it was written: Simulink, Matlab’s system dynamics program. This program is used by engineers all over the planet, and it is very expensive for non-academics. Getting a price upfront from Matlab is very difficult, but let’s say you won’t get much change out of $2,000 for an annual Simulink licence.

 

Figure 3: The Matlab Dashboard

Simulink has a lot of features and capabilities that Minsky doesn’t have, but there are shortcomings in its core functionalities that we’ve attempted to overcome in Minsky.

One is that, in Simulink, all calculations are passed “by wire”: if you want to use the output of one set of equations as an input to another, you have to draw a wire from one to the other. In Minsky, you can name the result of a set of equations—for example, “Die”—and then use that variable name elsewhere on the diagram, without needing to draw wires. This reduces model clutter compared to Simulink and almost all other system dynamics programs.

Figure 4: A Simulink model of a helicopter Flight Control System

Minsky also supports the mathematical formatting language LaTeX. In Simulink and to my knowledge all other system dynamics programs, if you want to use a variable called “”, you literally have to write the text “gamma”, and that’s what you see. In Minsky, you type \gamma, and what you see on its design canvas is . You can also use superscripts and subscripts, using the control characters _ and ^ respectively.

These are definite advances for Minsky, but if that were all there were to it, Minsky wouldn’t even exist. Minsky’s real reason for being is the unique double-entry bookkeeping feature we call “Godley Tables”. These are used to ensure that all financial flows are modelled properly, as having a source and a destination. Though our intention with the Godley Tables was to allow financial dynamics to be modelled easily, it also makes sense here when you are recording movements of people between different mutually exclusive categories. The first step in designing this Minsky model was to enter the total population (N) as an Asset, the number susceptible (S), Exposed (E), Infected (I) and Dead (D) as Liabilities, and those who have Recovered (R) as the Equity.

Minsky takes this as an input and generates the Ordinary Differential Equations automatically in the background. These are identical in structure to the equations in Figure 2, but the individual components have yet to be defined:

    

Figure 5: The initial equations in Minsky

The next step in building the model was to enter the parameters in the paper, and here there were two problems: they were scattered throughout the paper; and there were unnecessary steps taken by the authors that shows (I think!) that they are unfamiliar with the basic system dynamics concept of a time constant. This is a measure of how quickly a system state would take to reach a target level, expressed in the unit of time that makes sense for the system. With the Coronavirus, the sensible unit of time is a day, and one key “time constant” is how fast it takes for someone to go from being exposed to the disease to being actually infected. In the paper, this is called the incubation time, set at 5.1 days, and the symbol they use for it is .

This is all very sensible in system dynamics terms. The parameter is easily interpreted: if you increase its value to, say, 7, you are modelling the case where it takes about 7 days to get infected after exposure. Reduce it to 3, you are modelling where the process takes 3 days.

Unfortunately, they don’t use in their equations, but instead use , which they define on page 4 as “”. Then has the incomprehensible value of 0.196078. This is how I reproduced that in Minsky:

Figure 6: Defining as in Minsky

If I was doing this work myself and had the time, I would rewrite the equations in terms of time constants and get rid of this unnecessary step. But since I was doing this mainly to develop an instructional video for Bryan’s staff, I stuck with their equations and did this for several parameters in the model.

Figure 7: All the parameters in the model

The next step was to copy the stock (N,S,E,I,D, and R) and flow (Exp, Get, Die, Rec and Get_Again) variables from the Godley Table, which in common with so many aspects of Minsky, is on the right-mouse-button menu:

Figure 8: Copying the stock and flow variables onto the canvas

I didn’t complete the task—again, this was to instruct someone else in how to use Minsky rather than a job I intended doing from go to whoa—but I did complete a few of the definitions, including exposure, infection, and the death rates for the two different cohorts, young and over 65.

Figure 9: Defining Exposure and Infection in Minsky

Figure 10: Definitions for Die and Die_Old in Minsky

One thing that will prove a bit tricky for Bryan’s staff is the use of a time delay in the original model between when the disease and its first infections occur and when policy is developed:

Figure 11: The time delay of between the occurrence of the disease and infections and the policy response

Minsky doesn’t support time delays, largely for purist technical reasons. They introduce a discrete time element into a continuous time modelling framework, and I believe that discrete time modelling—dividing time into arbitrary units called “periods”—has been a major factor in Post Keynesian economics making far less progress in dynamics than it should have. So what you have to use instead is a first order time lag: you define another variable (say S_lag) and define this as something that converges to S with a lag. As an equation, this is:

    

Figure 12: First order time lag mathematics

As a Minsky flowchart, it is:

Figure 13: Implementing a first order time lag in Minsky

These variables S lag and I lag then replace and in the model:

    

This means that the Minsky model won’t quite match the simulation by the Simulink data, and some fine tuning will be needed to go from the delay they used (30 days) to a suitable time lag (I guessed at 14 days here). But those, in the customary words of the University lecturer, I leave as an exercise for the reader.

Over to you, Bryan and staff.

 

Merryn Somerset Webb has just recorded a podcast with me about the economic impact of the Coronavirus and what to do about it. This is a brief post to provide some of the data that I referenced in that discussion. Her podcasts are here, and the recording should be up soon.

While mainstream economists obsess about the level of government debt, the real cause of economic crises is not government debt but private debt. The UK’s data here is simply stunning. Between 1880 and 1982, private debt never exceeded 72% of GDP, and it averaged 57%. But it exploded after the deregulations that allowed the banking sector to lend to finance house purchases (and the privatisation of council housing and so on), rising to a peak of 195% of GDP in 2009.

That debt was split relatively equally between the household and corporate sector. After the 2008 crisis, both sectors have stabilized with almost three times the debt level, relative to GDP, that they had before financial deregulation.

The impact of that increased debt for the household sector has been simply higher house prices.

The causal mechanism runs from new mortgage debt to house prices. Putting it simply, most houses are bought primarily with mortgage debt, rather than out of income. So the monetary flow of demand for housing is primarily the flow of new mortgage debt. Divide this by the number of houses for sale, and you have a rough measure of the average demand price per house. Given how inflexible the supply of housing is, the change in this flow of demand is the primary determinant of the change in the house price level. So all this additional debt has done is simply drive up house prices by higher leverage.

This in turn has made Western nations in particular far more financially vulnerable than they were at the time of the last pandemic, in 1918, when private debt levels in the UK were at a historic low of 33% of GDP. With interest rates almost as low as today back then, the debt servicing burden on the economy was 1/5^th of what it is today.

This is why a proposal that I put forward as long ago as 2012—a “Modern Debt Jubilee”—is essential. Without it—and without income support from the government right now as well—the financial system could well collapse. A Twitter correspondent called it a “Universal Basic Bailout”, and that’s not a bad description in modern terms.

I’ll post this now and edit later to include an updated version of the argument I first made 8 years ago for a Modern Debt Jubilee. For now, to see the concept, please follow this link.

A friend on a discussion group I’m part of asked me this morning about the impact of debt repayment on the money supply:

So how does money and debt work in reverse? Has there ever been a deflation model based in real data… You know what you teach about how money is created by banks, what’s it look like in reverse, is money extinguished in deflation like money is created during inflation. If banks can lend money into existence using credit, does it work in reverse and can it be exponential?

That was easy to answer, since I’ve already modelled this extensively in Minsky:

Debt repaid reduces demand and money just as new debt creates both. Bankruptcy does the same via a fall in bank equity. Search for Patreon posts on loanable funds versus endogenous money [this is one of the posts I was thinking of why I wrote this] and you’ll see an instance.

It’s my Keen model on steroids. You could do the double entry in Minsky; I’m thinking off trying myself. Set up a multi bank model (3 should be enough) with rent from capitalists and landlords to banks, then halve the cash flow of both and see what happens. Halve output per worker as well.

The “Keen model” I referred to, as it’s now known in the literature, is my 1995 model of Minsky’s Financial Instability Hypothesis, where a series of credit-financed booms & busts leads to a final bust where debt repayment overwhelms the economy & causes a total economic collapse (click here for an accessible PDF). That is too complicated for what I want to examine here, but the alternative model in Minsky is looking pretty complicated as well. Here’s a first pass, with four banks—one each for firms, capitalists, landlords and workers—plus a Central Bank and a Treasury

 

What I’m planning on doing is setting up the financial flows so that the model-economy hums along OK, though with a high level of private debt (mimicking current US data, which for those who haven’t seen it before, is reproduced below:

Then I’ll introduce a “Coronavirus shock” that causes both output and employment to collapse, and see what happens to the solvency of the social classes in the model, as well as to the banks themselves.

Finally, I’ll bring in a “Modern Debt Jubilee“—both in a timely fashion, as soon as the Coronavirus shock hits, and belatedly.

The motivation of course is that policy ideas that I always thought had less than a snowflake’s chance in Hell of being implemented are now not merely being discussed but are, to some extent, being trialled in many parts of the world. This is not because the politicians and policy advisors who are doing this have read my posts of course: it’s simply that when something as serious as the Coronavirus strikes, the conventional wisdoms (of Neoclassical economics!) get thrown out the window as people panic, and find that what they used to say was either impossible or stupid is now both possible and sensible.

I’d be very pleased if other people here who are skilled at modelling in Minsky have a crack at this as well, either by editing the model I’ve attached here, or by working on their own. Global leaders are really flying blind right now, and maybe one of them will take a look at the work we do here.

 

There are many pundits arguing against government action now, on the basis that it will cause hyperinflation, and/or give our children an unsustainable burden of government debt to carry in the future. Here is a sample of such assertions.

Coronavirus hyperinflation risk looms, buy gold: Peter Schiff (USA, Fox News, March 25^th)

The extreme measures taken by the U.S. government and the Federal Reserve to combat the COVID-19 pandemic could push the U.S. into an episode of hyperinflation and boost gold, according to Peter Schiff.

Hysteria has forced the UK into lockdown, crashed the economy and will kill more than coronavirus (UK, The Sun, March 29^th)

Hysteria has been fanned by broadcasters with round-the-clock 24/7 crisis bulletins and correspondents declaring: “Protecting public health must come before protecting the economy.”

Wrong. We MUST protect the economy — industry, commerce, retail and financial businesses without whose taxes our precious NHS will shrivel, not grow.

The cost of this lockdown on schools, sport, gyms, pools, golf and civil liberty is incalculable — and not just in hard cash.

We are building a colossal national debt which will take our children’s and grandchildren’s lifetimes to pay off.

Helicopters? Bailouts? Central banks move to stem coronavirus crisis (Reuters, April 3^rd)

BUT ARE CENTRAL BANKS RISKING HIGH INFLATION?

The idea of central banks helping governments spend more has raised concerns about a rise in inflation and even drawn parallels with the disastrous hyperinflation of 1930s Germany and 1990s Zimbabwe.

Central bankers dismiss such comparisons, saying those cases involved unstable governments printing notes and handing them out to the public.

But JP Morgan strategist Jan Loeys said that if central banks eventually shift from their existing bond-buying programmes to direct funding of government spending, then inflation – which is currently low – might reawaken.

Bank of England won’t print more money to help tackle coronavirus – Governor Andrew Bailey (UK The Express, April 6^th)

“It would also ultimately result in an unsustainable central bank balance sheet and is incompatible with the pursuit of an inflation target by an independent central bank.”

The idea of central banks helping governments to spend more using monetary financing, whereby a central bank prints new money for governments to use rather than the governments acquiring money through taxation or borrowing has raised concerns about a rise in inflation in the future.

It has even drawn parallels with the disastrous hyperinflation of 1930s Germany and 1990s Zimbabwe.

There is no doubt that we’re in an unprecedented situation in economics as well as in health—one look at the US initial weekly unemployment claims data is enough to confirm that. So it’s quite possible that applying any existing experience or any existing theory—including mine—could lead to conclusions that turn out to be wildly wrong.

That said, my expectations are that, in the absence of the sort of government rescues that are now being tried around the world, the likely outcome of this crisis is serious deflation. This will be caused by a mechanism that I call “Fisher’s Paradox”, in honour of Irving Fisher, who first identified it as the primary cause of the Great Depression.

Fisher argued that the Great Depression was caused by the twin coincidence of too high a level of private debt, and too low a level of inflation. In this situation, debtors resorted to distress selling, cutting their prices in order to attract a cash flow to themselves rather than their competitors. But because everyone was doing it, prices fell across the board, taking GDP down with it. Debts therefore fell less than GDP, and the private debt ratio actually rose. In his words:

if the over-indebtedness with which we started was great enough, the liquidation of debts cannot keep up with the fall of prices which it causes. In that case, the liquidation defeats itself. While it diminishes the number of dollars owed, it may not do so as fast as it increases the value of each dollar owed. Then, the very effort of individuals to lessen their burden of debts increases it, because of the mass effect of the stampede to liquidate in swelling each dollar owed. Then we have the great paradox which, I submit, is the chief secret of most, if not all, great depressions: The more the debtors pay, the more they owe. The more the economic boat tips, the more it tends to tip. It is not tending to right itself, but is capsizing. “The Debt-Deflation Theory of Great Depressions” (Fisher 1933, p. 344)

Fisher’s Paradox was ignored by mainstream economics, because they subscribe to the fantasy model of banking known as “Loanable Funds”, in which banks are simply intermediaries between savers and borrowers. Fisher was not so stupid (well, not after he was effectively bankrupted by the Great Crash of 1929 anyway). Unlike today’s idiotic mainstream economists—here’s looking at you, Ben Bernanke (Bernanke 2000) and Paul Krugman, amongst many others—Fisher knew that a bank debt was very different to a debt between one non-bank and another:

the payment of a business debt owing to a commercial bank involves consequences different from those involved in the payment of a debt owing from one individual to another. A man-to-man debt may be paid without affecting the volume of outstanding currency. for whatever currency is paid by one, whether it be legal tender or deposit currency transferred by check, is received by the other, and is still outstanding. But when a debt to a commercial bank is paid by check out of a deposit balance that amount of deposit currency simply disappears. Booms and Depressions: Some First Principles (Fisher 1932, p. 15)

The empirical data bears Fisher out: America’ private debt to GDP ratio rose between 1929 and 1933 while the level of private debt was actually falling:

The raw dollar numbers make it even more obvious what happened: GDP fell faster than private debt:

As Fisher argued, the fall in the price level amplified the impact of the decline in real output. Falling prices combined with falling output to mean that the fall in nominal GDP was actually bigger than the fall in real (inflation-adjusted) GDP. Since debts are also measured in nominal terms, the fall in the price level made the rise in the private debt ratio worse: “the more debtors pay, the more they owe”.

This is why reflation, by Roosevelt’s New Deal (and also his “Bank Holidays”, which allowed insolvent banks to be wound up and their depositors funds transferred to solvent ones), was so important. If the injection of new money by the government hadn’t happened, this private sector chain reaction of liquidation leading to falling prices and an ever-rising debt level could have continued unabated: “The more the economic boat tips, the more it tends to tip. It is not tending to right itself, but is capsizing.”

I don’t care whether you’re a raving Austrian (Hi Peter!) or a raving Marxist, you don’t want this to happen. This is Hyman Minsky’s Financial Instability Hypothesis in the absence of a government sector, and as I showed in my PhD thesis and 1995 paper (Keen 1995), the end result is an economy with an infinite private debt ratio and zero employment.

What’s the relevance of this historical story to today’s situation? It is that the Coronavirus crisis has hit when we still haven’t addressed the runup of private debt that caused the Great Recession in 2007. Private debt today is higher than it was at the peak of the Great Depression.

We are therefore on the brink of a debt-deflation, and our policymakers don’t even know it because they take advice from Neoclassical economists who don’t understand the role of private debt and credit in the economy. We need a Modern Debt Jubilee now, or otherwise the damage the Coronavirus is doing to our health and capacity to produce now will be followed by the devastation of our financial system as well.

With the Coronavirus smashing both wages and profits in the US and global economies, the last thing we need is for workers that can’t pay their rents and mortgages, and firms that can’t pay their rents and service their corporate debts, to go bankrupt now. Inflation, which is already low, will turn negative, and the private debt ratio will explode once more, as it did in 1930-1933. Bankruptcies would cause a chain reaction of further failures, taking the banks down as well as the debtors. There would be no floor, especially since the Coronavirus has smashed not just demand but supply as well. Money would be destroyed by both the attempt of debtors to service their debts, and by the collapse of the banking sector as almost all debts turned bad.

So even if a massive injection of government money now would cause inflation in the future, the alternative is far, far worse.

References

Bernanke, B. S. (2000). Essays on the Great Depression. Princeton, Princeton University Press.

Fisher, I. (1932). Booms and Depressions: Some First Principles. New York, Adelphi.

Fisher, I. (1933). “The Debt-Deflation Theory of Great Depressions.” Econometrica
1(4): 337-357.

Keen, S. (1995). “Finance and Economic Breakdown: Modeling Minsky’s ‘Financial Instability Hypothesis.’.” Journal of Post Keynesian Economics
17(4): 607-635.

 

 

A lot of people still don’t seem to get the concept of exponential growth, even though we’ve had over two months of watching an exponential process unfold with the Coronavirus. I hope some simple illustrations using current data might help.

John Hopkins University is doing an excellent job of collating the cumulative number of cases reported around the world with its GIS database Coronavirus COVID-19 Global Cases by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU). They’ve made the raw time series data available too. Aggregated to the world level, this is what cumulative COVID-19 cases looked like as of late on April 4^th:

This is simply the total number of recorded cases, which includes tested cases where the carrier has only mild symptoms, people who got the disease way back when it began and have since recovered, those who have died, those who are still in intensive care, etc. The global total was just over 1.2 million on April 4^th.

A simple regression of this data onto an exponential function yields the prediction that, if the rate of transmission and the rate of doubling of the disease reflects what has happened to date from January 21^st, when the JHU time series begins, in a week’s time there will be twice as many cases: 2.5 million compared to today’s 1.2 million.

That’s a lot of cases, but it’s still way short of the total world population of about 7.5 billion. It took about ten weeks to go from 555 cases (the number recorded on January 21^st at the start of this data series) to over 1 million. How long will it take to get to a significant number compared to the planet’s population—say, half a billion cases?

It will take about another 8 weeks.

The red line in each of these graphs is the same red line.

Now only a fraction of those infected are going to be current cases—basically, those who were identified in the preceding 2-4 weeks—and only a fraction of those—perhaps about 20%–are going to require hospitalization. But that’s still a huge number of people, far more than can be handled in the world’s emergency medical facilities.

This is why this disease is not “just another flu”. It is far more contagious (and we also don’t have any innate resistance to it). We have to “Flatten the curve”, we can’t cope with the number of cases doubling every week, as is the case now.