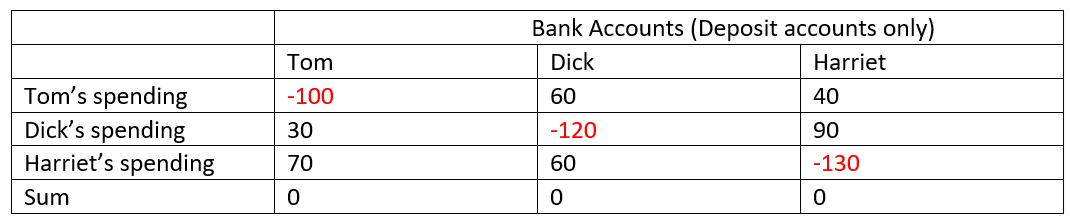
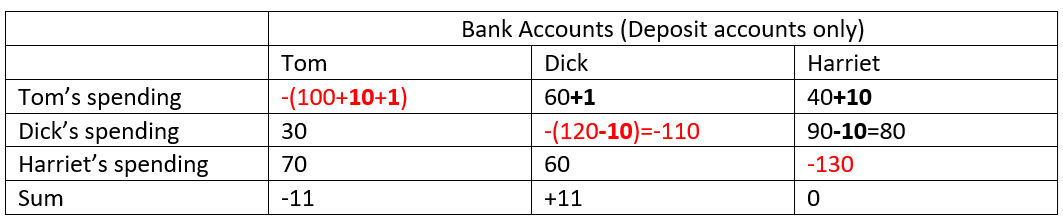
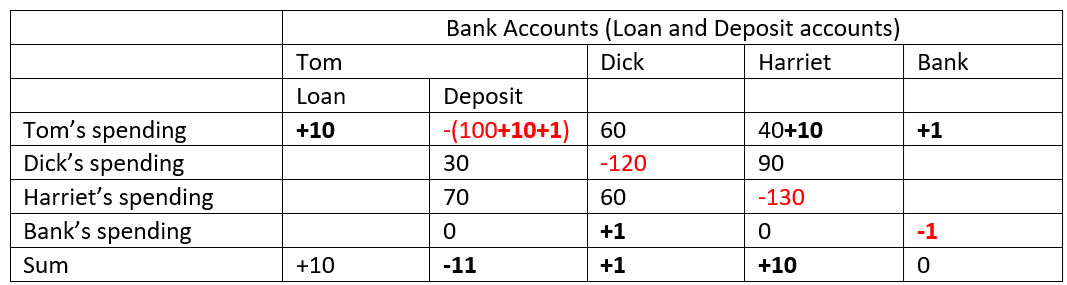
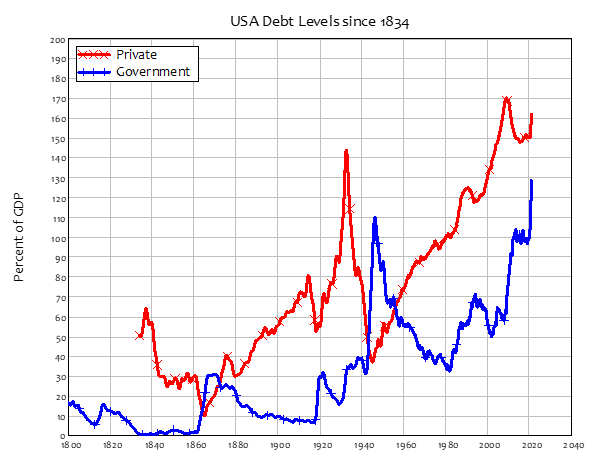
What are three things that the firms “Hungry Helen’s Cookie Factory”, “Thirsty Thelma’s Lemonade Stand”, “Big Bob’s Bagel Bin”, “Caroline’s Cookie Factory”, and “Conrad’s Coffee Shop” have in common? One thing is obvious: the use of alliteration in their names. A second, less obvious, is that they don’t in fact exist: instead, they are all fictional firms, used by Gregory Mankiw in various editions of his market-leading textbook Microeconomics (Mankiw 2001, 2009), to illustrate what are supposed to be common characteristics in the cost structure of actual firms.
The final commonality, known to very few people, is that these fictional firms have cost structures that are, in fact, nothing like those that of real firms. All of Mankiw’s fictional firms have relatively low fixed costs, and relatively high and rapidly rising variable costs—see Figure 1 for a representative example.
Figure 1: Figure 4 from Chapter 13 of (Mankiw 2009), p. 277

However, every survey ever done of the cost structure of actual firms has found the opposite: the vast majority of firms report have relatively high fixed costs, and relatively low and gradually falling marginal and average variable costs.
Why is there a clash between fact and fiction here, when Mankiw explicitly states that, by studying his fictional firms, “we can learn some lessons about costs that apply to all firms in an economy” (Mankiw 2009, p. 268)? It is because, if the actual cost structure of firms were used, then the economic theory of how firms decide how much to produce would fail. As the last economist to conduct a detailed survey of actual firms stated:
The overwhelmingly bad news here (for economic theory) is that, apparently, only 11 percent of GDP is produced under conditions of rising marginal cost. Almost half is produced under constant MC … But that leaves a stunning 40 percent of GDP in firms that report declining MC functions…
Firms report having very high fixed costs—roughly 40 percent of total costs on average. And many more companies state that they have falling, rather than rising, marginal cost curves. While there are reasons to wonder whether respondents interpreted these questions about costs correctly, their answers paint an image of the cost structure of the typical firm that is very different from the one immortalized in textbooks.” (Blinder 1998, pp. 102, 105. Emphasis added)
This economist provided a very ugly but still informative graphic illustrating the survey’s findings on marginal costs, which showed that only 11.1% of his survey respondents gave an answer on the shape of the marginal cost curve that was similar to that shown in Mankiw’s textbook—see Figure 2.
Figure 2: Figure 4.1 from (Blinder 1998), p. 103

This economist certainly has the authority to comment on the impact of this empirical reality on the validity of the textbook model of the firm, and its consequences for Neoclassical economics in general. Like Mankiw himself in all respects, Alan Blinder is a past-President of the Eastern Economic Association, served on the President’s Council of Economic Advisers, was a Vice President of the American Economic Association, and also publishes a highly influential economics textbook, Microeconomics: Principles and Policy (Baumol and Blinder 2011; Baumol and Blinder 2015).
Figure 3: Mankiw and Blinder in 2005 at Paul Samuelson’s 90th birthday party. Photo by Robert J. Gordon.

Does this mean that students of economics are getting a wildly different picture of the cost structure of firms, depending on whether their instructor chooses Mankiw, or Baumol and Blinder, as the textbook? No, it doesn’t—they both get the same picture! This is because, despite having done research which shows that almost 90% of firms have falling or constant marginal costs, Blinder’s textbook makes the same assumption as Mankiw’s, that rising marginal cost is the rule for all companies—see Figure 4. He makes no mention of his own empirical research that contradicts this assumption.
Figure 4: Figure 4(c) from Chapter 7 of (Baumol and Blinder 2011), p. 133

Why would a textbook writer who knows, from empirical research that he conducted, that this picture is false, nonetheless reproduce it? It is because, as Blinder himself stated, his empirical research was “overwhelmingly bad news … for economic theory”. Blinder clearly decided that, where theory and reality conflict, to stick with theory over reality.
Let’s consider that theory to see why he had to either make this decision, or cease being a Neoclassical economist.
The Neoclassical theory of rising marginal cost
The Neoclassical theory of production divides time into two divisions—the short-run and the long-run. It treats some inputs to production as fixed during the short-run, and others as variable, while in the long run, all inputs are treated as variable. The obvious choice for a fixed input in the short-run is capital—factories and machinery—while the only variable input considered, in most economic models as well as in textbooks, is labour.
Table 1 shows Mankiw’s numbers for “Caroline’s Cookie Factory”. The key feature of this Table that generates the outcome of rising marginal cost is the falling amount of additional output generated by each additional worker. The “Marginal Product of Labor” starts at 50 units for the first worker—from 0 cookies per hour with no workers, to 50 per hour with one worker—and falls to 5 additional cookies added by the 6th worker.
Table 1: Mankiw’s “Carolyn’s Cookies” fictional example (Mankiw 2009, p. 271)

This is the phenomenon of
“diminishing marginal productivity”, which, in Neoclassical theory, is the sole cause of rising marginal cost. The theory assumes that workers have uniform individual productivity, and that they can be hired at the same wage rate (because the individual firm is too small to affect the wage rate). With a constant cost per worker, the only source of rising marginal cost is falling output per worker, as more workers attempt to produce output with the same amount of machinery. This means that the data in Table 1 can be rearranged to show marginal cost for “Caroline’s Cookie Factory”—see Table 2, where I have calculated marginal revenue and profit as well by assuming the market price for a cookie is 75 cents, which—in keeping with the model of “perfect competition” (Keen 2004, 2005; Keen and Standish 2006, 2010)—is unaffected by the output level of Caroline’s firm.
Table 2: Marginal and total cost data derived from Table 1

Diminishing marginal productivity is, therefore, pivotal to the theory. It arises, not because of any variation in the skill of each individual worker, but from the interaction of more workers with a fixed amount of machinery. Mankiw paints a picture of a firm getting so crowded as more workers are added that eventually, the workforce gets in its own way:
At first, when only a few workers are hired, they have easy access to Caroline’s kitchen equipment. As the number of workers increases, additional workers have to share equipment and work in more crowded conditions. Eventually, the kitchen is so crowded that the workers start getting in each other’s way. Hence, as more and more workers are hired, each additional worker contributes fewer additional cookies to total production. (Mankiw 2009, p. 273. Emphasis added)
Blinder makes a similar case with his fictional example of “Al’s Building Company”:
Returns to a single input usually diminish because of the “law” of variable input proportions. When the quantity of one input increases while all others remain constant, the variable input whose quantity increases gradually becomes more and more abundant relative to the others, and gradually becomes over-abundant… As Al uses more and more carpenters with fixed quantities of other inputs, the proportion of labor time to other inputs becomes unbalanced. Adding yet more carpenter time then does little good and eventually begins to harm production. At this last point, the marginal physical product of carpenters becomes negative. (Baumol and Blinder 2015, p. 124. Emphasis added)
Blinder’s example generates the standard textbook drawing, shown in Figure 4, of falling marginal cost for low levels of output as marginal product rises, followed by rising marginal cost as marginal product falls. This occurs because there is an optimal ratio of variable to fixed inputs. When the ratio of variable to fixed inputs is below this ratio, marginal product rises, and hence marginal cost falls. Past this point, marginal product falls and marginal cost rises. The standard situation assumed for these fictional firms is that demand is so high that the firm always operates with a higher than optimum ratio of variable inputs (Labour) to fixed inputs (Machinery), so that an increase in output necessitates a fall in marginal product, and, therefore, a rise in marginal cost. The rising section of the marginal cost curve where it exceeds the average variable costs then becomes the short-run supply curve of the competitive firm, as Mankiw states emphatically:
The competitive firm’s short-run supply curve is the portion of its marginal-cost curve that lies above average variable cost.(Mankiw 2009, p. 298)
This is why Blinder’s empirical finding that marginal cost is constant or falling for almost 90% of the firms he surveyed was “overwhelmingly bad news … for economic theory”. Firstly, it implies that diminishing marginal productivity does not apply in real-world factories. This of itself is a serious conundrum: why does something that appears so logical in theory turn out not to apply in practice? Secondly, a supply curve can’t be derived for such firms. If marginal cost is constant, then it equals average variable cost; if marginal cost is falling, then it is always lower than average variable cost. Either way, there is no “portion of its marginal-cost curve that lies above average variable cost”, and therefore no “supply curve”—or at least, not one that is based on the marginal cost curve.
Thirdly, any firm that did price at its marginal cost would lose money. Revenue would at best be equal to average variable cost for constant marginal cost, while for falling marginal cost, each additional sale would increase the firm’s losses, and its most profitable output level—if the market price was equal to its marginal cost, which is a frequently used assumption in both micro and macroeconomics today—would be zero.
Finally, with falling marginal cost, and a constant price that exceeds its average variable costs—which Neoclassical economists assume is the normal case for “competitive” firms in the short run—then the only sensible output target for the firm would be to produce at 100% capacity.
Declining marginal cost therefore makes no sense to a Neoclassical economist, because it implies rising marginal productivity. This seems nonsensical, given the twin conditions of a fixed capital stock and variable inputs: how can you add more variable inputs to the same fixed capital stock, and yet get rising productivity as output increases, rather than falling productivity? Surely the “law of diminishing returns” must apply?
But in fact, numerous surveys have found that, somehow, it must not apply. Fred Lee’s Post Keynesian Price Theory (Lee 1998) is the definitive overview of these numerous surveys, which without exception found that the typical firm has marginal costs that are either constant or falling right out to capacity output, and fixed costs that are high relative to variable costs. If fact is our guiding light then, the fact that survey after survey has resulted in businesses reporting that they have constant or falling marginal cost must mean that diminishing marginal productivity is a fiction—at least in the context of a modern industrial factory. But why?
Why Diminishing Marginal Productivity doesn’t apply to factories
The Italian-born Cambridge University non-mainstream economist Piero Sraffa provided a simple explanation almost a century ago, in the paper “The Laws of Returns under Competitive Conditions” (Sraffa 1926). For a number of very good reasons, factories almost always operate with excess capacity: they have more machinery than they have workers to operate it.
The simplest reason is economic growth itself. When a factory is first built in a growing economy, it must start with more capacity available than can be used when it opens, otherwise it is too small. If a firm builds a new factory to cover anticipated growth in demand for 10 years, in an industry it expects to grow at 3% per year, then when the factory opens, the firm will have 25% spare capacity. This capacity can take the form of machines that are idle, or production lines that are initially run at well below their maximum speed.
Secondly, as Janos Kornai emphasised (Kornai 1979; Kornai 1985), a firm in a competitive industry will have excess capacity in case one of its competitors stumbles, or in case its own marketing exceeds its expectations. Excess capacity is an essential element in the flexibility that a firm needs to be an effective competitor. Competition itself leads to this outcome, as individual firms collectively aim for shares of expected future sales that, in the aggregate, the entire industry cannot support: optimism about future sales and market share, rather than pessimism, is the default position for the managers of firms. This in itself leads to boom-bust cycles in most industries, which results in capacity utilization varying dramatically with the business cycle, while excess capacity is the rule at the aggregate level, as well as at the individual firm—see Figure 5.
Figure 5: Excess capacity in the USA never fell below 10%, even during the boom years of the late 60s https://fred.stlouisfed.org/series/TCU

As a factory expands output within its existing capacity, workers are hired in the proportion needed to bring idle machinery online. These machines are operated at the ideal ratio of variable inputs to fixed, rather than at above or below that ratio. Factories are also designed by engineers to be at their most efficient at full capacity, so as this level is approached, productivity per head will rise rather than fall.
A telling instance of this is recorded in Tesla’s 10K filing for January 2021, in which it noted that a lower level of output of solar roofs than planned led to higher unit costs and therefore much lower gross margins. Higher sales would have enabled a lower per-unit cost of production, and therefore a higher margin:
Gross margin for energy generation and storage decreased from 12% to 1% in the year ended December 31, 2020 as compared to the year ended December 31, 2019 primarily due to a higher proportion of Solar Roof in our overall energy business which operated at lower gross margins as a result of temporary manufacturing underutilization during product ramp.
In fact, the textbook story of a factory with more workers than are ideal for its installed capital is so far from reality that it is better described, not as a model, but as a (fractured) fairy tale.
In the real world, a well-designed and managed factory does not operate in the range where diminishing marginal productivity might apply—contrary to the assumptions of Neoclassical economists. Individual machines within that factory are also operated at their ideal variable input to fixed input ratio at all times (though the speed of operation may be varied as well—with higher speed bringing the machine closer to its optimum operating parameters, and if they are at the optimum, output is expanded by bringing more machines online). Consequently, as Sraffa put it in 1926:
Businessmen, who regard themselves as being subject to competitive conditions, would consider absurd the assertion that the limit to their production is to be found in the internal conditions of production in their firm, which do not permit of the production of a greater quantity without an increase in cost. (Sraffa 1926, p. 543)
Sraffa’s expectation was born out by a host of surveys, the last of which was undertaken by Alan Blinder. Mainstream economists have turned avoiding learning from these surveys into an art form. The most sublime such artwork is Blinder turning a blind eye his own research, but the most impactful was Friedman’s advice to economists to ignore similar research undertaken in the 1940s and 1950s.
Not Listening About Prices
A leading figure in this empirical research was Wilford Eiteman, who was both an academic economist and a businessman. This juxtaposition of roles led him to reject Neoclassical theory as factually incorrect:
Around 1940, Eiteman was teaching marginalism in principles of economics classes at Duke University when it occurred to him that as treasurer of a construction company he had set prices and talked with others who set prices and yet had never heard of any price-setter mentioning marginal costs. He quickly came to the conclusion that a price-setting based on equating marginal costs to marginal revenue was nonsense. (Lee 1998, Kindle Locations 1529-1531)
As well as writing papers on the logical reasons for declining marginal costs, Eiteman’s research (Eiteman 1945, 1947, 1948, 1953; Eiteman and Guthrie 1952) included a survey that presented the managers of firms with 8 drawings representing possible shapes of their short run average cost function. Only one of these matched the standard drawings in economics textbooks—see Figure 6.
Figure 6: Eiteman’s 3rd of 8 possible shapes for the average cost curve

Another two matched the situation that Eiteman knew from personal experience, of declining average costs right out to full capacity, or very near it—see Figure 7.
Figure 7: Eiteman’s 6th and 7th possible shapes for the average cost curve

Precisely one of Eiteman’s 334 survey respondents chose Figure 6. 203 nominated his 7th drawing as properly representing their average costs, while another 113 opted for his 6th. Amusingly, while Neoclassical economists see themselves as supporters of capitalism, actual capitalists, when informed of Neoclassical economic theory, thought Neoclassical economists were trying to undermine capitalism rather than support it. Eiteman noted this reaction by one businessman:
“‘The amazing thing is that any sane economist could consider No. 3, No. 4 and No. 5 curves as representing business thinking. It looks as if some economists, assuming as a premise that business is not progressive, are trying to prove the premise by suggesting curves like Nos. 3, 4, and 5.” (Eiteman and Guthrie 1952, p. 838)
Another critic, Richard Lester, asked his respondents at what level of output did they achieve maximum profits. All gave answers that contradicted the standard textbook model, with 80% of those answering reporting that maximum profits came at maximum output:
In the present study, a series of questions was asked regarding unit variable costs and profits at various rates of output. In reply to the question, “At what level of operations are your profits generally greatest under peacetime conditions?” 42 firms answered 100 per cent of plant capacity. The remaining 11 replies ranged from 75 to 95 per cent of capacity. (Lester 1946, p. 68)
These papers led to one of the most influential innovations in the history of economics. No, not a realistic model of the firm, obviously, but a methodological innovation: Milton Friedman’s mantra that “the more significant the theory, the more unrealistic the assumptions” (Friedman 1953, p. 153). Two of Friedman’s objectives with this paper were to stop research into models of the firm other than the two Neoclassical extremes of perfect competition and perfect monopoly, and to get economists to ignore empirical research challenging the assumption of diminishing marginal productivity:
The theory of monopolistic and imperfect competition is one example of the neglect in economic theory of these propositions. The development of this analysis was explicitly motivated .. by the belief that the assumptions of “perfect competition” or “perfect monopoly” said to underlie neoclassical economic theory are a false image of reality. And this belief was itself based almost entirely on the directly perceived descriptive inaccuracy of the assumptions rather than on any recognized contradiction of predictions derived from neoclassical economic theory. The lengthy discussion on marginal analysis in the American Economic Review some years ago is an even clearer, though much less important, example. The articles on both sides of the controversy largely neglect what seems to me clearly the main issue – the conformity to experience of the implications of the marginal analysis – and concentrate on the largely irrelevant question whether businessmen do or do not in fact reach their decisions by consulting schedules, or curves, or multivariable functions showing marginal cost and marginal revenue. (Friedman 1953, pp. 153-54. Emphasis added)
Friedman mischaracterised both of these research programmes, but especially the latter. He described the empirical research as being about whether businessmen actually use calculus in deciding output levels, when in fact it was about whether the conditions for this approach to work in the first place actually held. But this nuance didn’t matter to either Friedman, or the vast majority of Neoclassical economists, who simply did not want to hear what the empirical research was finding. They wanted to stick with their models of perfect competition and rising marginal cost, and Friedman’s methodological trick gave them a generic methodological reason to do so. When someone objected to the unreality of the model, they could sagely reply that it doesn’t matter that the assumptions of the theory of the firm are unrealistic, since “the more significant the theory, the more unrealistic the assumptions”:
the relation between the significance of a theory and the “realism” of its “assumptions” is almost the opposite of that suggested by the view under criticism. Truly important and significant hypotheses will be found to have “assumptions” that are wildly inaccurate descriptive representations of reality, and, in general, the more significant the theory, the more unrealistic the assumptions (in this sense)…
To put this point less paradoxically, the relevant question to ask about the “assumptions” of a theory is not whether they are descriptively “realistic,” for they never are, but whether they are sufficiently good approximations for the purpose in hand. And this question can be answered only by seeing whether the theory works, which means whether it yields sufficiently accurate predictions. The two supposedly independent tests thus reduce to one test. (Friedman 1953, p. 153. Emphasis added)
This is methodological nonsense. While it is passably true for genuine simplifying assumptions, it is utterly false when applied to justify assuming that firms experience rising marginal cost, when as a matter of empirical fact, they face constant or falling marginal cost.
A simplifying assumption is something which, if you don’t make it, results in a much more complicated model, which yields only a tiny improvement in its results over the simpler model.
For example, the Aristotelian belief that heavy objects fall faster than light ones was disproved by Galileo’s experiment, which showed that two dense objects of different weights fell at the same speed. Aristotelian physicists could have rejected Galileo’s proof on the grounds that his experiment ignored the effect of the air on how fast the objects fell. This would have forced Galileo to construct a much more elaborate experiment, but the outcome would have been almost exactly the same: the two objects of different weights would still have fallen at much the same rate, rather than the different rate that Aristotelian physics predicted. Galileo’s “assumption” that the experiment was conducted in a vacuum—which is easily classified as a “wildly inaccurate descriptive representation… of reality” (Friedman 1953, p. 153)—was a genuine simplifying assumption.
However, the assumption of rising marginal cost is instead an instance of what philosopher Alan Musgrave described as “domain assumptions” (Musgrave 1981). These are assumptions which, If they are true, mean that the theory applies, but if they are false, then it doesn’t. The assumption that marginal cost rises is not a mere simplifying assumption, but an assumption that is of critical importance to Neoclassical economic theory. If the assumption is false—which it manifestly is—then so is Neoclassical economics.
The critical importance of unrealistic assumptions
The Neoclassical profit maximization rule is to equate marginal revenue to marginal cost, assuming that the firm is producing past the point where average and marginal costs are rising. If marginal cost is rising, then marginal cost lies above average cost, and the firm makes a profit on every unit sold, right up until the point at which marginal cost equals price. For this reason, the marginal cost curve of a firm in a “perfectly competitive” industry is its supply curve: name a price, draw a line from that price out to the marginal cost curve, and the quantity the firm will supply at that price will be the quantity that equates its marginal cost to its marginal revenue, and thus maximizes its profit see (but see Keen and Standish 2010).
If marginal cost is falling however, then marginal cost is less than average cost. For the firm in a “perfectly competitive” industry, following the Neoclassical “profit-maximising” rule of equating marginal revenue to marginal cost results in a price that is therefore below average cost. At that price, the firm’s profit-maximising output level is zero. Therefore, there is no “supply curve” unless marginal cost is rising.
This is why Blinder’s empirical finding—that, for roughly 90% of firms, marginal cost is constant or falling right out to capacity output—was, as he put it, “overwhelmingly bad news … for economic theory”. This empirical fact means that the whole edifice of the Neoclassical theory of supply has to go. But that wasn’t what Blinder was looking for, let alone expecting, when he decided to ask firms about prices.
Asking About Prices—and then ignoring the answers
Hall and Hitch (Hall and Hitch 1939), Eiteman (Eiteman 1945, 1947, 1948; Eiteman and Guthrie 1952; Eiteman 1953), Lester (Lester 1946, 1947), Means (Means 1935, 1936, 1972; Tucker et al. 1938), and many others who have undertaken surveys of firms were critics of the Neoclassical model, and wanted to replace it with something more realistic. Blinder, au contraire, is solidly part of the Neoclassical establishment. His reason for undertaking his survey was not to question the mainstream, but to provide a firm foundation for “sticky prices”, which were an essential element of the “New Keynesian” faction of Neoclassical macroeconomists.
Self-described “New Classical” macroeconomists developed the approach of deriving macroeconomics directly from microeconomics, in which they assumed perfect competition throughout—and therefore, price equal to marginal cost. With rapid price adjustments, all of the impact of a change in aggregate demand was absorbed by a change in prices. In “Real Business Cycle” models therefore, the economy is in general equilibrium at all times, even during events like the Great Depression. Edward Prescott, one of the two originators of RBC modelling, argued that the cause of the huge rise in unemployment during the Great Depression was a voluntary decrease in the total number of hours of work that workers decided to supply, in response to unspecified changes in labour market regulations:
the Great Depression is a great decline in steady-state market hours. I think this great decline was the unintended consequence of labor market institutions and industrial policies designed to improve the performance of the economy. Exactly what changes in market institutions and industrial policies gave rise to the large decline in normal market hours is not clear. (Prescott 1999, p. 6)
This was too much for Neoclassical economists with some attachment to reality: unemployment during the Great Depression was not a utility-maximizing choice, but involuntary. Consequently, they developed Dynamic Stochastic General Equilibrium (DSGE) models, in which the slow adjustment of prices to equilibrium values was a key explanation of periods of involuntary unemployment. Blinder’s research was undertaken to find an empirically valid explanation for so-called “sticky prices”, within the overall confines of Neoclassical microeconomics:
In recent decades, macroeconomic theorists have devoted enormous amounts of time, thought, and energy to the search for better microtheoretic foundations for macroeconomic behavior. Nowhere has this search borne less fruit than in seeking answers to the following question: Why do nominal wages and prices react so slowly to business cycle developments? In short, why are wages and prices so “sticky”? The abject failure of the standard research methodology to make headway on this critical issue in the microfoundations of macroeconomics motivated the unorthodox approach of the present study. (Blinder 1998, p. 3)
The unorthodox aspect of his study was to actually conduct interviews—given that Friedman had disparaged the very idea of asking businessmen what they thought about their businesses:
The billiard player, if asked how he decides where to hit the ball, may say that he “just figures it out” but then also rubs a rabbit’s foot just to make sure; and the businessman may well say that he prices at average cost, with of course some minor deviations when the market makes it necessary. The one statement is about as helpful as the other, and neither is a relevant test of the associated hypothesis. (Friedman 1953, p. 158)
Blinder designed his study well to avoid the pitfalls expected by Friedman, so its results could not be dismissed as due to bad research procedures—and these results were similar to those reached by the earlier surveys that Friedman recommended economists not to read. But though Blinder knew his research methods were beyond reproach, he still found it hard to accept two of its key findings, that average fixed costs are high relative to average variable costs, and that marginal cost does not rise for the typical firm:
Third, firms typically report fixed costs that are quite high relative to variable costs (question AI2). And they rarely report the upward-sloping marginal cost curves that are ubiquitous in economic theory. Indeed, downward-sloping marginal cost curves are more common, according to the survey responses (question B 7 [a] ). If these answers are to be believed—and this is where we have the gravest doubts about the accuracy of the survey responses—then the whole presumption that prices should be strongly pro-cyclical is called into question. (Blinder 1998, p. 302)
His very next sentence showed why he had difficulty in accepting these answers. If they were true, then much of mainstream economic theory was false:
But so, by the way, is a good deal of microeconomic theory. For example, price cannot approximate marginal cost in a competitive market if fixed costs are very high. (Blinder 1998, p. 302)
In the end, fealty to conventional theory trumped Blinder’s personal exposure to the contrary data of facts. His denial of his own research findings in his textbook is so remarkable as to be worth citing at length:
The “law” of diminishing marginal returns, which has played a key role in economics for two centuries, states that an increase in the amount of any one input, holding the amounts of all others constant, ultimately leads to lower marginal returns to the expanding input.
This so-called law rests simply on observed facts; economists did not deduce the relationship analytically. Returns to a single input usually diminish because of the “law” of variable input proportions. When the quantity of one input increases while all others remain constant, the variable input whose quantity increases gradually becomes more and more abundant relative to the others, and gradually becomes over-abundant. (For example, the proportion of labor increases and the proportions of other inputs, such as lumber, decrease.) As Al uses more and more carpenters with fixed quantities of other inputs, the proportion of labor time to other inputs becomes unbalanced. Adding yet more carpenter time then does little good and eventually begins to harm production. At this last point, the marginal physical product of carpenters becomes negative.
Many real-world cases seem to follow the law of variable input proportions. In China, for instance, farmers have been using increasingly more fertilizer as they try to produce larger grain harvests to feed the country’s burgeoning population. Although its consumption of fertilizer is four times higher than it was fifteen years ago, China’s grain output has increased by only 50 percent. This relationship certainly suggests that fertilizer use has reached the zone of diminishing returns. (Baumol and Blinder 2015, p. 124. Emphasis added)
Blinder’s claim that the “law” was implied from empirical observation, rather than derived deductively, is simply untrue. The concept was first put in its Neoclassical form in 1911 by Edgeworth, where his table was, like Mankiw’s alliterated firms in today’s textbooks, a figment of Edgeworth’s imagination. To illustrate how mistaken Blinder is above, it is also worth quoting at length from Brue’s careful examination of the intellectual history of the concept of diminishing returns:
an explicit exposition of diminishing returns, distinguishing between the average and marginal products of a variable homogeneous input, had to await Francis Edgeworth and John Bates Clark.
In 1911 Edgeworth constructed a hypothetical table in which he assumed land was a fixed input (Edgeworth 1911, p. 355). The first two columns of the table related various levels of the “labor/tools” input with corresponding levels of total crops. In the third column, Edgeworth derived the marginal product of the variable input; in the fourth, the average product of the variable input. Thus, the values of the table demonstrated the relationships between total, marginal, and average product. Like his predecessors, Edgeworth drew his example from agriculture, not manufacturing. Nevertheless, he asserted that the idea was applicable in all industries…
Jacob Viner (1931 [1958], pp. 50–78) and others then developed the contemporary graphical link between the law of diminishing marginal returns and the firm’s marginal cost curves and short-run product supply curves. Since then, the law of diminishing returns has become the modern centerpiece for explaining upward-sloping product supply curves…
Along with circular and special-case proofs, none of the economists mentioned here marshalled strong empirical evidence to validate their propositions. Instead they stated the law as an axiom, offered specific examples, or referred to hypothetical data to demonstrate their point…
Menger (1936 [1954]) severely criticized the axiomatic acceptance of the law of diminishing returns, arguing that the crucial issue for economics is the empirical question of whether or not the laws of returns are true or false. His call for direct empirical verification of the law—and through extension, the rising short-run marginal cost curve—remains valid.
In his 1949 book Manufacturing Business, Andrews (pp. 82–111) introduced another complication relating to the law of diminishing returns and its applications. He argued that manufacturing firms maintain excess capacity so that they do not lose present customers in times of unexpected demand, have the capacity to cover for breakdowns of machinery, and take advantage of opportunities to capture new customers in a growing market. When excess capacity exists, the law of diminishing returns may have little relevance for cost curves. Firms can change short-run output simply by varying the hours of employment of the “fixed” plant proportionally with the variable inputs. The ratios of the inputs employed need not change and marginal cost need not rise…
However, it does seem clear that the history of economic theory has produced an axiomatic acceptance of the law of diminishing returns and rising marginal costs. More empirical investigation is needed on whether this law is operational under conditions of excess capacity, and how it is relevant to the burgeoning service industries. Conjectures by 19th century economists about input and outputs in agriculture simply won’t do! (Brue 1993, pp. 187-91. Emphasis added)
Blinder’s own examples also contradict his statement that “diminishing marginal returns” rests on “observed facts”. His first example is a fictional one, from his made-up example of Al’s Building Company. His second example, of the increased use of fertilizer in China over 15 years, violates the pre-conditions of diminishing marginal productivity, which only apply in the short-run when one factor of production is fixed.
This argument reeks of Blinder attempting to rationalise ignoring the results of his own research. His unexpected experience of what Thomas Huxley elegantly described as “the great tragedy of Science—the slaying of a beautiful hypothesis by an ugly fact” (Huxley 1870, p. 402), led to him to discard the ugly fact, so that he could remain faithful to the beautiful theory.
In fact, the theory is anything but beautiful, as a more critical examination of Blinder’s and Mankiw’s fictional examples exposes—see the Appendix. But the main problem is that it is simply wrong. Our theory of costs and prices should be based on reality rather than fantasy.
Real Cost Curves
The consistent points found in empirical research about actual firms are that:
- Average Fixed Costs are high. Whereas Neoclassical drawings—for that is all they are— put average fixed cost at 10-20% of total costs at maximum output, only ¼ of the firms Blinder surveyed picked a figure below 20%. The mean value was 44% of total costs, and 8% of firms reported average fixed costs at over 80% of total costs;
- Average Variable Costs are commensurately lower than in Neoclassical drawings, and generally fall rather than rise as output rises.
- Therefore, Marginal Cost typically lies below Average Variable Cost, and well below Average Total Cost.
Figure 8 shows an extreme example of this empirical norm—using hypothetical data, because I don’t have access to commercial data, but with the characteristics of this hypothetical case fitting Blinder’s survey results, rather than contradicting them, as Blinder does in his textbook. These are cost curves for a silicon wafer manufacturing firm, based loosely on Samsung’s major plant, with Fixed Costs of $33 billion, an assumed cost of capital of 5% (the same as Mankiw used in his examples), Average Fixed Costs being 85% of total costs at maximum output, and declining variable costs, beginning at $1600 per wafer and falling to $1344 at capacity output of 744,000 wafers per year. This is roughly consistent with price being an estimated 100% markup on costs per wafer, and prices in the realm of $5000 per wafer for high-end wafers.
Figure 8: Hypothetical costs for a silicon wafer foundry

Marginal cost is irrelevant to the output decision here, while the profit-maximizing output level is 100% of capacity. Price also far exceeds marginal cost.
Neoclassical economics could cope with this situation if it could regard this as an example of a “natural monopoly”, where declining costs make a competitive structure impossible—but the numerous surveys have all found that the vast majority of firms in all industries report a similar cost structure. This implies that price both substantially exceeds marginal cost, and is indeed unrelated to it, in all industry structures.
What the theory of supply should be
The false Neoclassical assumption of diminishing marginal productivity is a critical component of the Neoclassical theory of supply. It goes hand in hand with the eulogising of “perfect competition”, the demonising of “monopoly”, and the analysis of intermediate structures—”imperfect competition”, “oligopoly”—by means of game theory. It is vital to the claim that competitive markets achieve a social optimum of marginal benefit equalling marginal cost, and that other market structures are inferior because they result in output levels where marginal benefit exceeds marginal cost.
It is also a serious impediment to understanding real competition. In the real world, where almost all firms face declining average costs as output rises, and market capacity significantly exceeds market demand in normal times, the emphasis is on achieving higher sales than the breakeven level, and targeting the maximum sales volume possible. This is done via product development and differentiation, aided by marketing that focuses on the qualitative differences between the firm’s product and those of its competitors. Falling average cost with production volume gives the firm capacity to discount as sales increase, and allow price to fall as sales rise—the opposite of the Neoclassical model, and consistent with the results of numerous surveys of business practice.
This real process of competition could explain why the real world size distribution of firms bears absolutely no resemblance to the Neoclassical taxonomy of “perfectly competitive, imperfectly competitive, oligopolistic, monopolistic” industries, but instead has many small firms co-existing in industries with a few large firms. This empirical regularity (which is known as a Power Law, Zipf Law or Pareto Law distribution), results in the log of a measure of the size of a firm being negatively related to the log of how many firms are that size in an industry or country (Axtell 2001, 2006; Fujiwara et al. 2004; Heinrich and Dai 2016; Montebruno et al. 2019).
This is readily seen in the aggregate US data—see Table 3, which shows the 2014 data from the United States Small Business Administration (SBA) on the number of firms by the number of employees per firm (the data covers all firms in the USA, but the SBA provides detailed statistics only for firms with 500 or less employees).
Table 3: Number of US firms and size of firms in 2014 (https://www.sba.gov/sites/default/files/advocacy/static_us_14.xls)

Figure 9 shows the characteristic linear relationship between the log of size and log of frequency that turns up in Power Law distributions.
Figure 9: The Power Law behind the size distribution data in Table 3

This kind of distribution abounds in nature as well as in economic data (Axtell 2001; Di Guilmi et al. 2003; Malamud and Turcotte 2006; Gabaix 2009). It is the hallmark of the evolutionary dynamics that should be the focus of economics, in marked contrast to the sterile taxonomy of non-existent industry market structures that both defines and bedevils Neoclassical microeconomics.
Conclusion
The Neoclassical theory of the supply curve as the sum of the rising marginal cost curves of firms in a perfectly competitive industry is thus a fiction, right from the foundational concept of diminishing marginal productivity. Its origins lie, not in the real world, but in its role as a reflection of the Neoclassical theory of the demand curve, where “diminishing marginal utility” is the foundational concept. When diminishing marginal utility in a rational, utility maximizing consumer, meets diminishing productivity in a rational, profit-maximizing firm, we get the Neoclassical nirvana of marginal benefit equalling marginal cost, and therefore free-market capitalism as the social system that best maximises utility, subject to the cost constraint.
This is why Neoclassicals cling so religiously to the concepts of diminishing marginal productivity, and rising marginal cost, despite overwhelming empirical evidence to the contrary (Sraffa 1926; Hall and Hitch 1939; Eiteman 1947; Eiteman and Guthrie 1952; Means 1972; Blinder 1998; Lee 1998). If they admit that the norm is constant or rising marginal productivity, and constant or falling marginal cost, then the two halves of Neoclassical economics no longer fit together. Better bury the empirical evidence (Friedman 1953) or ignore it (Baumol and Blinder 2015), rather than to accept it, and have to abandon Neoclassical economics instead.
We should have no such qualms. The Neoclassical theory of the firm is the economic equivalent of the theory of Phlogiston that chemists once used to explain combustion, before the discovery of oxygen. Economists discovered their oxygen almost a century ago now, firstly in the logical work of Sraffa in 1926 (Sraffa 1926) and then the empirical work of the Oxford Economists’ Research Group, which commenced in 1934 (Lee 1998, Chapter 4). It’s well past time that we threw out the economic equivalent of Phlogiston, the belief in “diminishing marginal productivity” as a characteristic of industrial capitalism, and developed a realistic theory of firms, industries, and competition.
And if this involves abandoning Neoclassical economics as well, then so much the better.
Appendix: The real shape of fictional cost curves
You will recall that shows Table 2 shows the per-unit costs that can be derived from Mankiw’s fictional production data for “Caroline’s Cookie Factory”, shown in Table 1. Figure 10 graphs those numbers. This Figure has characteristics that should be readily apparent to anyone who has ever even glanced at an economics textbook.
Figure 10: Cost curves derived from Mankiw’s production numbers in Table 1

Firstly, this diagram is ugly: it looks nothing like the (relatively) beautiful curves Mankiw shows for cost curves in the same chapter—see Figure 1, Error! Reference source not found. and Error! Reference source not found. here. They all look fine in comparison to Figure 10.
Secondly, notice that the numbers on Figure 1 are very small—maxing out at 10 units per hour—while there are no numbers on the axes of Error! Reference source not found. or Error! Reference source not found.. Why not?
The clue to this puzzle is the values on the Quantity axis for Mankiw’s total cost curve plot (Figure 11 below), and the Quantity axis for his demonstration of rising marginal cost (Figure 12). Notice that the Quantity Axis for “Hungry Helen’s” total cost curve Figure 11 has a maximum of 150 units per hour—not a big number, but OK if we’re imagining a numerical example of a single firm in a “perfectly competitive” market.
Figure 11: Mankiw’s Figure 13-3, on page 275

Now check the Quantity axis on Figure 12, which supposedly shows the cost structure for another “typical” firm, “Thirsty Thelma’s”: it maxes out at just ten units per hour: a decidedly small number. Why doesn’t Mankiw use a more reasonable number, like he did in the penultimate figure?
Figure 12: Mankiw’s Figure 13-5, on page 279

It gets curiouser still. Mankiw has not one graph of total cost, but two—see Figure 11 and Figure 13. Why?
Figure 13: Mankiw’s Figure 13-4, on page 276

It is, I expect, because Mankiw tried using the data from “Hungry Helen’s” to derive the average and marginal cost curves, but found that the graph looked ugly—it looked, in other words, like my Figure 10. This simply wouldn’t do in a textbook that pays more attention to appearance than its content, so he tried lower numbers for another made-up firm, “Thirsty Thelma’s”, and that worked. Rather than getting rid of the whole previous section—with “Hungry Helen’s” higher output numbers—he just left it in there, resulting in two superficially identical figures for Total Cost. Again, why?
This puzzle has a numerical solution, which explains a bizarre feature of Neoclassical textbook examples of the cost structure of firms: when they show drawings derived from made-up data, the quantity numbers are trivial. Mankiw, as noted, has a maximum output of ten units per hour in his “Thirsty Thelma’s” example (see Figure 12); Blinder has 10 garages per year as his maximum output level for the cost curves in “Al’s Building Company” (Baumol and Blinder 2011, pp. 132-134)—see Figure 4—even though he earlier had his fictional company producing up to 35 garages per year in his exposition of the production function (Baumol and Blinder 2011, p. 124).
The answer is that the shapes of archetypical average and marginal cost drawings that abound in Neoclassical texts—where Average Variable Costs are about five times Average Fixed Costs at the maximum output level shown on the drawing, while the rapidly-falling segment of Average Fixed Cost is also visible on the diagram—require Fixed Cost to be very small. If large output numbers are used, the resulting curves will look nothing like the archetypical shape.
To understand this, firstly note that, since marginal cost and variable cost curves are treated as continuous functions, they can be approximated by polynomials. Secondly, marginal cost (MC) is the derivative of variable cost (VC) with respect to quantity Q, and average cost (AVC) is variable cost VC divided by Q: see Equations and :


Since AVC and MC can be expressed as polynomials, they are therefore polynomials of the same order: all they differ by are their coefficients. In turn, these coefficients are related by a simple rule, that the coefficient for the nth power of a marginal cost term must be times the coefficient for the same term in average variable cost. For example, if marginal cost (MC) is a quadratic, then so is average variable cost (AVC), and the coefficient for the term in MC will be three times the coefficient for the term in AVC—see Equation :

Average Fixed Cost AFC, on the other hand, is a reciprocal function:

To make polynomial functions of Q appear on the same scale as an inverse function of Q, the value of Q can’t be too big—hence the crazily small numbers used for output in numerically derived Neoclassical drawings. I doubt that this numerical fudging was deliberate, because Neoclassicals are not aware of these limitations on the shape of cost functions for their preferred model. I suspect instead that these authors tried arbitrarily chosen values for Fixed Cost with large values for , unexpectedly got ugly drawings like Figure 10, and went on to use smaller values for , without realising why those drawings worked better than those with larger values.
References
Axtell RL (2001) Zipf Distribution of U.S. Firm Sizes. Science (American Association for the Advancement of Science) 293 (5536):1818-1820. doi:10.1126/science.1062081
Axtell RL (2006) Firm Sizes: Facts, Formulae, Fables and Fantasies.
Baumol WJ, Blinder A (2011) Microeconomics: Principles and Policy. 12th edn.,
Baumol WJ, Blinder AS (2015) Microeconomics: Principles and policy. 14th edn. Nelson Education,
Blinder AS (1998) Asking about prices: a new approach to understanding price stickiness. Russell Sage Foundation, New York
Brue SL (1993) Retrospectives: The Law of Diminishing Returns. Journal of Economic Perspectives 7 (3):185-192. doi:10.1257/jep.7.3.185
Di Guilmi C, Gaffeo E, Gallegati M (2003) Power Law Scaling in the World Income Distribution. Economics Bulletin 15 (6):1-7. doi:http://www.economicsbulletin.com/
Edgeworth FY (1911) Contributions to the Theory of Railway Rates. The Economic journal (London) 21 (83):346-370. doi:10.2307/2222325
Eiteman WJ (1945) The Equilibrium of the Firm in Multi-Process Industries. THE QUARTERLY JOURNAL OF ECONOMICS 59 (2):280-286
Eiteman WJ (1947) Factors Determining the Location of the Least Cost Point. The American Economic Review 37 (5):910-918
Eiteman WJ (1948) The Least Cost Point, Capacity, and Marginal Analysis: A Rejoinder. The American Economic Review 38 (5):899-904
Eiteman WJ (1953) The Shape of the Average Cost Curve: Rejoinder. The American Economic Review 43 (4):628-630
Eiteman WJ, Guthrie GE (1952) The Shape of the Average Cost Curve. The American Economic Review 42 (5):832-838
Friedman M (1953) The Methodology of Positive Economics. In: Essays in positive economics. University of Chicago Press, Chicago, pp 3-43
Fujiwara Y, Di Guilmi C, Aoyama H, Gallegati M, Souma W (2004) Do Pareto–Zipf and Gibrat laws hold true? An analysis with European firms. Physica A 335 (1):197-216. doi:10.1016/j.physa.2003.12.015
Gabaix X (2009) Power Laws in Economics and Finance. Annual Review of Economics 1 (1):255-293. doi:http://arjournals.annualreviews.org/loi/economics/
Garrett TJ, Grasselli M, Keen S (2020) Past world economic production constrains current energy demands: Persistent scaling with implications for economic growth and climate change mitigation. PLoS ONE 15 (8):e0237672. doi:https://doi.org/10.1371/journal.pone.0237672
Hall RL, Hitch CJ (1939) Price Theory and Business Behaviour. Oxford Economic Papers (2):12-45
Heinrich T, Dai S (2016) Diversity of firm sizes, complexity, and industry structure in the Chinese economy. Structural change and economic dynamics 37:90-106. doi:10.1016/j.strueco.2016.01.001
Huxley TH (1870) Address of Thomas Henry Huxley, L.L.D., F.R.S., President. Nature 2 (46):400-406
Keen S (2004) Deregulator: Judgment Day for Microeconomics. Utilities Policy 12:109-125
Keen S (2005) Why Economics Must Abandon Its Theory of the Firm. In: Salzano M, Kirman A (eds) Economics: Complex Windows. New Economic Windows series. Springer, Milan and New York: , pp 65-88
Keen S, Ayres RU, Standish R (2019) A Note on the Role of Energy in Production. Ecological Economics 157:40-46. doi:https://doi.org/10.1016/j.ecolecon.2018.11.002
Keen S, Standish R (2006) Profit maximization, industry structure, and competition: A critique of neoclassical theory. Physica A: Statistical Mechanics and its Applications 370 (1):81-85
Keen S, Standish R (2010) Debunking the theory of the firm—a chronology. Real World Economics Review 54 (54):56-94
Kornai J (1979) Resource-Constrained versus Demand-Constrained Systems. Econometrica 47 (4):801-819
Kornai J (1985) Fix-Price Models: A Survey of Recent Empirical Work: Comment. In: Arrow KJ, Honkapohja S (eds) Frontiers of Economics. Oxford and New York:
Blackwell, pp 379-390
Lee FS (1998) Post Keynesian Price Theory. Cambridge University Press, Cambridge
Lester RA (1946) Shortcomings of Marginal Analysis for Wage-Employment Problems. The American economic review 36 (1):63-82
Lester RA (1947) Marginalism, Minimum Wages, and Labor Markets. The American economic review 37 (1):135-148
Malamud BD, Turcotte DL (2006) The applicability of power-law frequency statistics to floods. Journal of Hydrology 322 (1-4):168-180. doi:DOI: 10.1016/j.jhydrol.2005.02.032
Mankiw NG (2001) Principles of Microeconomics. 2nd edn. South-Western College Publishers, Stamford
Mankiw NG (2009) Principles of Microeconomics. 5th edn. South-Western College Publishers, Mason, OH
Means GC (1935) Price Inflexibility and the Requirements of a Stabilizing Monetary Policy. Journal of the American Statistical Association 30 (190):401-413
Means GC (1936) Notes on Inflexible Prices. The American Economic Review 26 (1):23-35
Means GC (1972) The Administered-Price Thesis Reconfirmed. The American Economic Review 62 (3):292-306
Montebruno P, Bennett R, Van Lieshout C, Smith H (2019) A tale of two tails: Do Power Law and Lognormal models fit firm-size distributions in the mid-Victorian era? doi:10.17863/CAM.37178
Musgrave A (1981) ‘Unreal Assumptions’ in Economic Theory: The F‐Twist Untwisted. Kyklos (Basel) 34 (3):377-387. doi:10.1111/j.1467-6435.1981.tb01195.x
Prescott EC (1999) Some Observations on the Great Depression. Federal Reserve Bank of Minneapolis Quarterly Review 23 (1):25-31
Sraffa P (1926) The Laws of Returns under Competitive Conditions. The Economic Journal 36 (144):535-550
Tucker RS, Bernheim AL, Schneider MG, Means GC (1938) Big Business, Its Growth and Its Place. Journal of the American Statistical Association 33 (202):406-411